《2025年课时训练九年级数学上册苏科版江苏人民出版社》

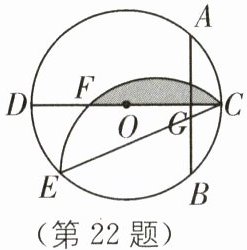
22. (8分)如图,CD是$\odot O$的直径,AB是$\odot O$的弦,$AB⊥CD$,垂足为G,$OG:CG= 3:2,AB= 16$.
(1)求$\odot O$的半径;
(2)点E为圆上一点,若$∠ECD= 30^{\circ }$,将$\widehat {CE}$沿弦CE翻折,交CD于点F,求图中阴影部分的面积.

答案：

(1)如图，连接AO.
∵CD为$\odot O$的直径，AB⊥CD，AB=16，
∴AG=$\frac{1}{2}$AB=8.
　　　　　　　　　　　　　　　　
∵OG:CG=3:2，
∴OG:OC=3:5.
　设$\odot O$的半径为5k，则OG=3k，
∴(3k)²+8²=(5k)²，
　解得k=2或k=−2(舍去)，
∴5k=10.故$\odot O$的半径是10.
(2)如图，将阴影部分沿CE翻折，点F的对应点为M，连接OM、CM.由对称性可知，
∵∠ECD=30°，
∴∠DCM=60°，S_阴影=S_弓形CBM，
∴∠MOD=120°，
∴∠MOC=60°.
　　过点M作MN⊥CD于点N，则MN=$5\sqrt{3}$，
∴S_阴影=S_扇形OMC-S_△OMC=$\frac{60\pi×10^2}{360}-\frac{1}{2}×10×5\sqrt{3}=\frac{50\pi}{3}-25\sqrt{3}$.

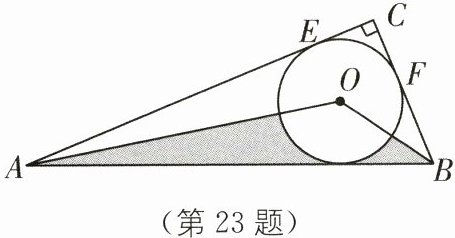
23. (8分)如图,在$Rt\triangle ABC$中,$∠ACB= 90^{\circ },AC= 12,BC= 5$,半径为2的$\odot O$分别与AC、BC相切于点E、F.
(1)求证:AB是$\odot O$的切线;
(2)求图中阴影部分的面积.

答案：

(1)如图，连接OE、OF、OC，作OM⊥AB，垂足为M.
　　　　　　
∵$\odot O$与AC、BC相切，
∴OE=OF=2，∠OEC=∠OFC=90°.
　　在Rt△ABC中，AB=$\sqrt{AC^2+BC^2}=\sqrt{12^2+5^2}$=13，根据面积法，得S_△AOC+S_△BOC+S_△AOB=S_△ABC，
　　即$\frac{1}{2}$OE·AC+$\frac{1}{2}$OF·BC+$\frac{1}{2}$OM·AB=$\frac{1}{2}$AC·BC，
∴OM=2.
　　又OM⊥AB于点M，
∴AB是$\odot O$的切线
(2)
∵OM⊥AB，∠OEC=∠OFC=90°，OE=OF=OM，
∴OA、OB分别是∠CAB、∠CBA的平分线，
∵∠ACB=90°，
∴∠CAB+∠CBA=90°，
∴∠OAB+∠OBA=45°，
∴∠AOB=135°，
∴S_阴影=S_△AOB-S_扇形=$\frac{1}{2}×13×2-\frac{135\pi×2^2}{360}=13-\frac{3}{2}\pi$.