《2025年课时训练七年级数学上册苏科版江苏人民出版社》

1 教材P125例4·改编 若三角形三个角的度数比为$3:3:4$,则这个三角形一定是(A).
A.锐角三角形
B.直角三角形
C.钝角三角形
D.无法确定

答案： A

2 甲、乙两瓶中分别有水4升和10升,现要从这两瓶中各倒一些水到空的丙瓶中,使三个瓶中水量的比为$3:2:1$,那么乙瓶需倒出水3或$5\frac{1}{3}$升.

答案： 3或$5\frac{1}{3}$

3 如图,已知长方形ABCD的长$AD= 12$,宽$AB= 9$,内有边长相等的小正方形AIGJ和小正方形ELCK,它们的重叠部分为长方形EFGH.若长方形EFGH的周长为14,则正方形ELCK的面积为(D).
A.156
B.144
C.81
D.49

答案： D

4 (2024·镇江句容期末)将长度分别为2dm和3dm的两根细铁丝分别围成长方形甲和长方形乙(接缝处忽略不计),使这两个长方形的长相等,如果将二者等长的边重合,恰好拼成一个正方形,那么这个正方形的边长为$\frac{5}{6}$dm.

答案： $\frac{5}{6}$

5 幻方是我国的一种传统游戏,要求将数安排在方格中,使每行、每列及对角线上的3个数的和都相等.例如,在图(1)所示的幻方中,每行、每列及对角线上的3个数之和均为15.
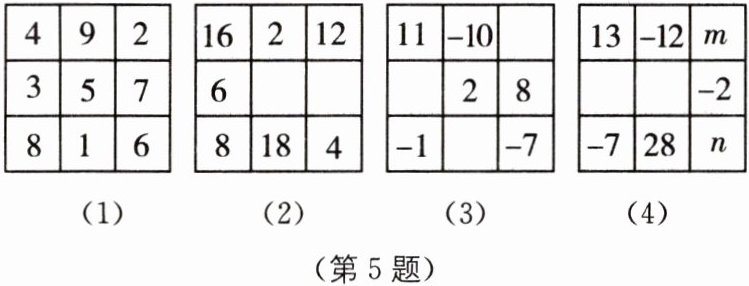
(1)如图(2),请在两个空白方格中填上适当的数,以满足幻方游戏的要求;
(2)如图(3),请在三个空白方格中填上适当的数,以满足幻方游戏的要求;
(3)如图(4),试求幻方中m,n的值.

答案：

(1)设两个空白方格中填上的数是x,y,如图， 根据游戏规则,得16+6+8=2+x+18=12+y+4,解得x=10,y=14,
∴两个空白方格中填上的数是10和14.
(2)由题图知，幻方每行、每列及对角线的3个数之和均为11+2−7=6,
∴最上面一行最后一个数为6−(11-10)=5,中间一行第一个数为6−(2+8)=−4,最下面一行中间一个数是6−(−1−7)=14,
∴三个空白方格中填上的数分别是5，−4和14.
(3)根据游戏规则可得13−12+m=−7+28+n,
∴m=n+20.由最下面一行与最右边一行的和相等可得−7+28+n=m−2+n,
∴−7+28+n=(n+20)−2+n,解得n=3,
∴m=n+20=23.故m的值为23,n的值为3.

(1)如图,用一个正方形框在表中任意框住4个数,记左上角的一个数为x,则另三个数用含x的式子表示出来,从小到大依次是x+1,x+7,x+8.
(2)当(1)中被框住的4个数之和等于216时,x的值为多少?
x+(x+1)+(x+7)+(x+8)=216,解得x=50.
∵7×7=49＜50＜8×7=56,
∴50是第8行第1个数，
∴x=50符合题意.
(3)在(1)中能否框住这样的4个数,它们的和等于156? 若能,则求出x的值;若不能,则说明理由.
不能.理由如下:假设能框住这样的4个数，它们的和等于156,则x+(x+1)+(x+7)+(x+8)=156,解得x=35.
∵35是第5行最后一个数，
∴x=35不符合题意，故不能框住这样的4个数，它们的和等于156.

答案：
(1)x+1　x+7　x+8 [解析]根据题意，可得左上角的一个数为x，则另三个数用含x的式子表示为x+1,x+7,x+8.
(2)x+(x+1)+(x+7)+(x+8)=216,解得x=50.
∵7×7=49＜50＜8×7=56,
∴50是第8行第1个数，
∴x=50符合题意.
(3)不能.理由如下:假设能框住这样的4个数，它们的和等于156,则x+(x+1)+(x+7)+(x+8)=156,解得x=35.
∵35是第5行最后一个数，
∴x=35不符合题意，故不能框住这样的4个数，它们的和等于156.