《2025年课时训练七年级数学上册苏科版江苏人民出版社》

12 如果a和$1-4b$互为相反数,那么多项式$2(b-2a+10)+7(a-2b-3)$的值是(A).
A.-4
B.-2
C.2
D.4

答案： A

13 作差法 已知$A= 2x^{2}-3y^{2}+1,B= x^{2}-5y^{2}-5$,则代数式A和B的关系是(A).
A.$A＞B$
B.$A＜B$
C.$A= B$
D.不能确定

答案： A

14 老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,形式如$\overbrace{}^{2}-(2x^{2}-2x+1)= -x^{2}+6x-3$,则所捂住的多项式是$x^{2}+4x-2$.

答案： $x^{2}+4x-2$

15 先化简,再求值:$4a^{2}+3(b^{2}-2ab)-2(2a^{2}-ab)$,其中$a= -\frac {1}{2},b= -2.$

答案： 原式$=4a^{2}+3b^{2}-6ab-4a^{2}+2ab=-4ab+3b^{2}.$当$a=-\frac {1}{2},b=-2$时，原式$=-4×(-\frac {1}{2})×(-2)+3×(-2)^{2}=-4+12=8.$

16 (2024·镇江期末)先化简,再求值:$-2xy+(5xy-3x^{2}+1)-3(2xy-x^{2})$,其中x,y满足$|x+2|+(y-1)^{2}= 0.$

答案： $-2xy+(5xy-3x^{2}+1)-3(2xy-x^{2})=-2xy+5xy-3x^{2}+1-6xy+3x^{2}=-3xy+1.$$\because x,y$满足$|x+2|+(y-1)^{2}=0,\therefore |x+2|=0,(y-1)^{2}=0$,即$x+2=0,y-1=0,\therefore x=-2,y=1$.当$x=-2,y=1$时，原式$=-3×(-2)×1+1=7.$

17 (2025·南京玄武区期末)如图,公园有一块长为$(2m-2)$米,宽为m米的长方形土地(一边靠墙),现将三边留出宽都是n米的小路,余下部分设计成花圃ABCD,用篱笆把花圃不靠墙的三边围起来.

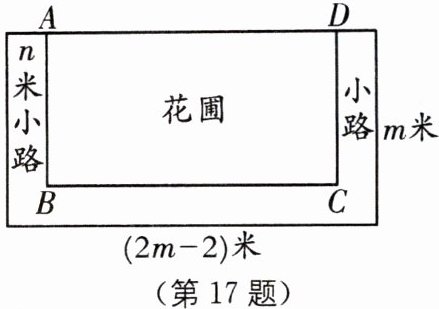
(1)花圃的宽AB为$(m-n)$米,花圃的长BC为$(2m-2n-2)$米(用含m,n的式子表示);
(2)求篱笆的总长度(用含m,n的式子表示);
(2)$2(m-n)+(2m-2n-2)=2m-2n+2m-2n-2=(4m-4n-2)$米.
(3)若$m= 29,n= 6$,篱笆的单价为60元/米,请计算篱笆的总价.
(3)将$m=29,n=6$代入$4m-4n-2,$得$4m-4n-2=4×29-4×6-2=92-2=90,$篱笆的总价为$90×60=5400$(元).故篱笆的总价是 5400 元.

答案：
(1)$(m-n)$ $(2m-2n-2)$
(2)$2(m-n)+(2m-2n-2)=2m-2n+2m-2n-2=(4m-4n-2)$米.
(3)将$m=29,n=6$代入$4m-4n-2,$得$4m-4n-2=4×29-4×6-2=92-2=90,$篱笆的总价为$90×60=5400$(元).故篱笆的总价是 5400 元.

18 中考新考法 看错改错问题 在数学课上,老师给出了一道题目:“先化简,再求值:$(x^{2}+□x-1)-3(\frac {1}{3}x^{2}-2x+4)$,其中$x= -1$”,□中的数据被污染,无法解答,只记得□中是一个实数,于是老师即兴出题,请同学们回答:
(1)化简后的代数式中常数项是多少?
(2)若点点同学把“$x= -1$”看成了“$x= 1$”,化简求值的结果仍不变,求此时□中数的值.
(3)若圆圆同学把“$x= -1$”看成了“$x= 1$”,化简求值的结果为-3,求当$x= -1$时,正确的代数式的值.

答案：
(1)设□中的数据为a，则$(x^{2}+ax-1)-3(\frac {1}{3}x^{2}-2x+4)=x^{2}+ax-1-x^{2}+6x-12=(a+6)x-13.$故化简后的代数式中常数项是-13.
(2)$\because$化简求值的结果不变，$\therefore -(a+6)-13=a+6-13,\therefore a+6=0,\therefore a=-6.$故此时□中的值为-6.
(3)由题意，得当$x=1$时，$(a+6)x-13=-3,\therefore a+6-13=-3,\therefore a=4,\therefore$当$x=-1$时，$(a+6)x-13=-4-6-13=-23.$故当$x=-1$时，正确的代数式的值为-23.