《2025年课时训练七年级数学上册苏科版江苏人民出版社》

10 如果$a,b$互为相反数,$c,d$互为倒数,$|m|= 2,|n|= 1$,且$mn＜0$,那么式子$(mn)^{3}-(a+b)^{2025}+(-cd)^{2025}$的值是(D).
A.$7$
B.$-7$
C.$9$
D.$-9$

答案： D

11 用“数字牌”做$24$点游戏,抽出的四张牌分别表示$5,-6,7,-8$(每张牌只能用一次,可以用加、减、乘、除运算),请写出一个算式,使结果为$24$:(5+7)×[(-6)-(-8)]=24.

答案： (5+7)×[(-6)-(-8)]=24(答案不唯一)

12 中考新考法 规律探究 已知$a＞0,S_{1}= \frac {1}{a},S_{2}= -S_{1}-1,S_{3}= \frac {1}{S_{2}},S_{4}= -S_{3}-1,S_{5}= \frac {1}{S_{4}},…$(即当$n为大于1$的奇数时,$S_{n}= \frac {1}{S_{n-1}}$;当$n为大于1$的偶数时,$S_{n}= -S_{n-1}-1$).按此规律,当$a= 2$时,$S_{2025}= $-$\frac{2}{3}$.

答案： -$\frac{2}{3}$ [解析]当a=2时,$S_1=\frac{1}{2}$,$S_2=-S_1-1=-\frac{1}{2}-1=-\frac{3}{2}$,$S_3=\frac{1}{S_2}=-\frac{2}{3}$,$S_4=-S_3-1=-(-\frac{2}{3})-1=-\frac{1}{3}$,$S_5=\frac{1}{S_4}=-3$,$S_6=-S_5-1=-(-3)-1=2$,$S_7=\frac{1}{S_6}=\frac{1}{2}$,…,
∴由此可得,所得的数列每6个一循环.
∵2025=337×6+3,
∴$S_{2025}=S_3=-\frac{2}{3}$.

13 (2024·湖北黄冈期末改编)计算:
(1)$(-\frac {1}{36})÷(\frac {1}{6}-\frac {1}{9}-\frac {1}{3})$;
(2)$-1^{2025}×[2-(-3)^{2}]+3÷(-\frac {3}{4})$.

答案：
(1)$\frac{1}{10}$
(2)3

14 中考新考法 满足结论的条件开放 如图,小明有$5$张写着不同数字的卡片,请你按要求抽出卡片,完成下列问题:

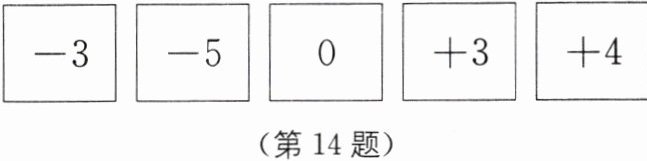
从中取出$4$张卡片,用学过的运算方法,使结果为$24$.如何抽取? 请写出运算式子.(写出三种)

答案： 答案不唯一,如:[0-(-3)+3]×4=24;[0-(-3)-(-5)]×3=24;[(3-(-5)]×[0-(-3)]=24.

(1)下列运算满足“反换律”的是②.(填序号)
①加法,②减法,③除法.
(2)规定“⊕”运算:$a⊕b= a^{2}+b^{2}-3ab$.
①若$a= 1,b= -2$,则$a⊕b=$11;
②请你判断“⊕”运算是否满足“反换律”,并说明理由.
满足.理由如下:
∵$a⊕b=a^2+b^2-3ab$,
∴$(-b)⊕(-a)=(-b)^2+(-a)^2-3×(-b)×(-a)$$=b^2+a^2-3ab$$=a^2+b^2-3ab$,
∴$a⊕b=(-b)⊕(-a)$,
∴“⊕”运算满足“反换律”.

答案：
(1)② [解析]
∵$a+b≠-b+(-a)$,
∴加法不满足"反换律";
∵$a-b=-b-(-a)$,
∴减法满足"反换律";
∵$a÷b≠-b÷(-a)$,
∴除法不满足"反换律".
(2)①11 [解析]$a⊕b=a^2+b^2-3ab$=1^2+(-2)^2-3×1×(-2)=11.②满足.理由如下:
∵$a⊕b=a^2+b^2-3ab$,
∴$(-b)⊕(-a)=(-b)^2+(-a)^2-3×(-b)×(-a)$=a^2+b^2-3ab,
∴$a⊕b=(-b)⊕(-a)$,
∴"⊕"运算满足"反换律".