《2025年课时训练七年级数学上册苏科版江苏人民出版社》

1 观察算式$(-4)×\frac{1}{7}×(-25)×14$,在解题过程中,能使运算变得简便的运算律是(C)。
A.乘法交换律
B.乘法结合律
C.乘法交换律、结合律
D.乘法对加法的分配律

答案： C

计算$(-99\frac{32}{33})×33$,最合理的方法是(C)。
A.$(-99\frac{32}{33})×33= (-99-\frac{32}{33})×33$
B.$(-99\frac{32}{33})×33= (-99+\frac{32}{33})×33$
C.$(-99\frac{32}{33})×33= (-100+\frac{1}{33})×33$
D.$(-99\frac{32}{33})×33= (-100-\frac{1}{33})×33$

答案： C

3 计算$(\frac{1}{2}-\frac{5}{6}+\frac{5}{12}-\frac{7}{24})×24$的结果是(D)。
A.-2
B.-3
C.-4
D.-5

答案： D

(1)$(-4)×6= 6×$(-4)；
(2)$[(-3)×2]×(-5)= (-3)×[$(2)$×$(-5)]；
(3)$(-6)×[\frac{1}{2}+(-\frac{1}{3})]= (-6)×$$\frac{1}{2}$+$(-6)×$$(-\frac{1}{3})$。

答案：
(1)-4
(2)2 -5
(3)$\frac{1}{2}$ $(-\frac{1}{3})$

5 计算：$4×(-8.99)×(-2.5)= $89.9。

答案： 89.9

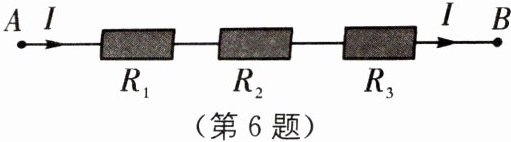
6 跨学科 电路 (2024·广州中考)如图,把$R_1$,$R_2$,$R_3$三个电阻串联起来,线路AB上的电流为I,电压为U,则$U= IR_1+IR_2+IR_3$,当$R_1= 20.3$,$R_2= 31.9$,$R_3= 47.8$,$I= 2.2$时,U的值为 220。

答案： 220

7 教材P47练习T1·改编 计算：
(1)$-\frac{3}{5}×(-2)×(-15)$；
(2)$(-0.125)×(-\frac{4}{7})×8×(-7)$；
(3)$(-2\frac{1}{4})×(-\frac{5}{6})×\frac{2}{3}×(-28)$。

答案：
(1)-18
(2)-4
(3)-35

8 教材P47练习T2·改编 (2025·苏州工业园区期末)-2025的倒数是(D)。
A.2025
B.-2025
C.$\frac{1}{2025}$
D.$-\frac{1}{2025}$

答案： D

9 已知 ×$(-\frac{2}{3})= 1$,那么 内应填的数是(A)。
A.$-\frac{3}{2}$
B.$-\frac{2}{3}$
C.$\frac{3}{2}$
D.$\frac{2}{3}$

答案： A

10 (2024·湖北黄冈期末)若m,n互为相反数,a,b互为倒数,则$|m-5+n|+ab= $6。

答案： 6

11 教材P47例3·变式 计算：
(1)$(-2\frac{1}{3})×(-\frac{3}{7})$；(2)$2\frac{1}{2}×(-\frac{2}{5})$。

答案：
(1)原式=$(-\frac{7}{3})×(-\frac{3}{7})=1.$
(2)原式=$-(\frac{5}{2}×\frac{2}{5})=-1.$