《2025年课时训练七年级数学上册苏科版江苏人民出版社》

8 如图,已知点A是射线BE上一点,过点A作$AC⊥BF$,垂足为C,过点C作$CD⊥BE$,垂足为D. 给出下列结论：
①$∠1是∠ACD$的余角；
②图中互余的角共有3对；
③$∠1的补角只有∠DCF$；
④与$∠ADC$互补的角共有3个.
其中正确的结论是①④.(填序号)

答案： ①④

9 直线$AB⊥CD$,垂足为O,直线EF经过点O,若锐角$∠COE= m^{\circ }$,则$∠AOF= $$(90 - m)$或$(90 + m)$°.(用含m的代数式表示)

答案： $(90 - m)$或$(90 + m)$

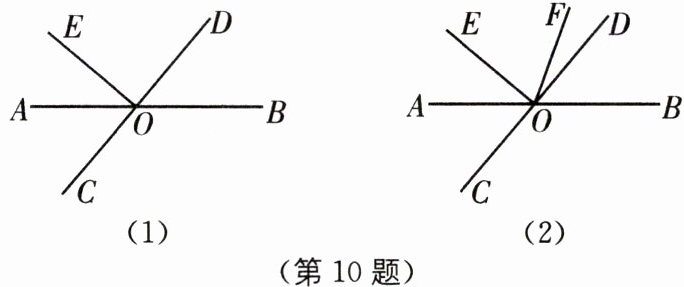
10 如图,直线AB与CD相交于点O,射线OE在$∠AOD$的内部,$∠AOC= 70^{\circ }-\frac {1}{2}∠AOE$.
(1)如图(1),当$∠AOE= 40^{\circ }$时,请写出与$∠BOD$互余的角,并说明理由；
(2)如图(2),若OF平分$∠BOE$,求$∠DOF$的度数.
]

答案：
(1)
∵$∠AOC = 70^{\circ } - \frac{1}{2}∠AOE$，$∠AOE = 40^{\circ }$，
∴$∠AOC = 70^{\circ } - \frac{1}{2}×40^{\circ } = 50^{\circ }$，
∴$∠BOD = ∠AOC = 50^{\circ }$，
∴$∠BOD + ∠AOE = 50^{\circ } + 40^{\circ } = 90^{\circ }$，
　　即$∠AOE$与$∠BOD$互为余角.
(2)
∵OF平分$∠BOE$，
∴$∠BOF = ∠EOF = \frac{1}{2}∠BOE$.
∵$∠AOE + 2∠BOF = 180^{\circ }$，
∴$∠AOE + 2∠DOF + 2∠BOD = 180^{\circ }$.
∵$∠AOC = 70^{\circ } - \frac{1}{2}∠AOE = ∠BOD$，
∴$∠AOE + 2∠DOF + 140^{\circ } - ∠AOE = 180^{\circ }$，
　　即$∠DOF = 20^{\circ }$.

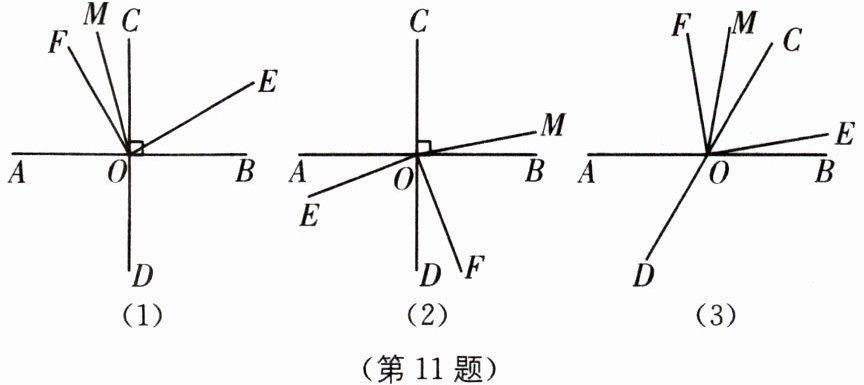
11 中考新考法 分类讨论 (2024·南京玄武区期末)直线AB,CD相交于点O,$∠EOF= 90^{\circ }$,射线OM平分$∠COF$.(本题中所有角的度数均不超过$180^{\circ }$)
(1)若$AB⊥CD$.
①将$∠EOF$绕点O旋转至图(1)的位置,$∠BOE= 30^{\circ }$,则$∠AOM= $______°.
②将$∠EOF$绕点O旋转至图(2)的位置,$∠AOM与∠BOE$有怎样的数量关系？请说明理由.
(2)如图(3),若$∠BOC= 60^{\circ }$,将$∠EOF$绕点O顺时针旋转一周,请直接写出在整个旋转过程中$∠AOM与∠BOE$的数量关系.
]

答案：

(1)①75
　②$2∠AOM = ∠BOE + 180^{\circ }$.理由如下：
∵$AB⊥CD$，
∴$∠AOD = ∠BOD = ∠AOC = 90^{\circ }$，
∵$∠EOF = 90^{\circ }$，
∴$∠AOE = 90^{\circ } - ∠EOD = ∠DOF$.
∵OM平分$∠COF$，
∴$∠COM = \frac{1}{2}∠COF = \frac{1}{2}(180^{\circ } - ∠DOF) = 90^{\circ } - \frac{1}{2}∠DOF$，
∴$∠AOM = ∠AOC + ∠COM = 90^{\circ } + 90^{\circ } - \frac{1}{2}∠DOF = 180^{\circ } - \frac{1}{2}∠DOF$，
∴$2∠AOM = 360^{\circ } - ∠DOF$.
∵$∠BOE = 180^{\circ } - ∠AOE = 180^{\circ } - ∠DOF$，
∴$2∠AOM = ∠BOE + 180^{\circ }$.
(2)设$∠COM = ∠FOM = \alpha$，
　如图
(1)：
　　　　　　　
∵$∠BOC = 60^{\circ }$，
∴$∠AOC = 120^{\circ }$，
∴$∠AOM = ∠AOC - ∠COM = 120^{\circ } - \alpha$，
∴$2∠AOM = 240^{\circ } - 2\alpha$.
∵$∠BOE = 180^{\circ } - ∠EOF - ∠AOF$，
∴$∠BOE = 180^{\circ } - 90^{\circ } - (120^{\circ } - 2\alpha ) = 2\alpha - 30^{\circ }$，
∴$2∠AOM + ∠BOE = 210^{\circ }$；
　如图
(2)：
　　　　　
∵$∠BOM = ∠COM - ∠BOC = \alpha - 60^{\circ }$，
∴$∠AOM = 180^{\circ } - ∠BOM = 180^{\circ } - (\alpha - 60^{\circ }) = 240^{\circ } - \alpha$，
∴$2∠AOM = 480^{\circ } - 2\alpha$.
　又$∠BOF = ∠BOM + ∠FOM = \alpha - 60^{\circ } + \alpha = 2\alpha - 60^{\circ }$，
∴$∠BOE = 360^{\circ } - ∠BOF - ∠EOF = 360^{\circ } - (2\alpha - 60^{\circ }) - 90^{\circ } = 330^{\circ } - 2\alpha$，
∴$2∠AOM - ∠BOE = 150^{\circ }$；
　如图
(3)：
　　　　　
∵$∠BOM = \alpha - 60^{\circ }$，
∴$∠AOM = 180^{\circ } - ∠BOM = 240^{\circ } - \alpha$，
∴$2∠AOM = 480^{\circ } - 2\alpha$.
　又$∠BOF = 2\alpha - 60^{\circ }$，
∴$∠BOE = 2\alpha + 30^{\circ }$，
∴$2∠AOM + ∠BOE = 510^{\circ }$；
　如图
(4)：
　　　　　
∵$∠AOM = ∠AOC + ∠COM$，
∴$∠AOM = 120^{\circ } + \alpha$，
∴$2∠AOM = 240^{\circ } + 2\alpha$.
∵$∠BOM = ∠BOC - ∠COM = 60^{\circ } - \alpha$，
∴$∠BOF = ∠FOM - ∠BOM = \alpha - (60^{\circ } - \alpha ) = 2\alpha - 60^{\circ }$，
∴$∠BOE = ∠BOF + ∠EOF = 2\alpha - 60^{\circ } + 90^{\circ } = 2\alpha + 30^{\circ }$，
∴$2∠AOM - ∠BOE = 210^{\circ }$.
　综上所述，整个旋转过程中，$∠AOM$与$∠BOE$的关系为$2∠AOM + ∠BOE = 210^{\circ }$或$2∠AOM - ∠BOE = 150^{\circ }$或$2∠AOM + ∠BOE = 510^{\circ }$或$2∠AOM - ∠BOE = 210^{\circ }$.