《2025年课时训练七年级数学上册苏科版江苏人民出版社》

6 (2024·达州中考)如图,正方体的表面展开图上写有“我们热爱中国”六个字,还原成正方体后“我”的对面的字是(B).

A.“热”
B.“爱”
C.“中”
D.“国”

答案： B

7 (2024·江西中考)如图是$4×3$的正方形网格,选择一空白小正方形,能与阴影部分组成正方体展开图的方法有(B).

A.1种
B.2种
C.3种
D.4种

答案： B

8 (2024·德阳中考)走马灯,又称仙音烛,据史料记载,走马灯的历史起源于隋唐时期,盛行于宋代,是中国特色工艺品,常见于除夕、元宵、中秋等节日.在一次综合实践活动中,一同学用如图所示的纸片,沿折痕折合成一个棱锥形的“走马灯”,正方形做底,侧面有一个三角形面上写了“祥”字,当灯旋转时,正好看到“吉祥如意”的字样.则在A,B,C处依次写上的字可以是(A).
A.吉,如,意
B.意,吉,如
C.吉,意,如
D.意,如,吉

答案： A

9 如图,一个长方体的表面展开图中四边形ABCD是正方形,则原长方体的体积是187.5$\mathrm{cm}^{3}$.

答案： 187.5 [解析]
∵四边形 ABCD 是正方形,$\therefore AB=AD=10\ \text{cm}$.$\therefore$长方体的高为$(15-10)÷ 2=2.5(\text{cm})$.$\therefore$长方体的宽为$10-2.5=7.5(\text{cm})$.$\therefore$原长方体的体积是$7.5× 2.5× 10=187.5(\text{cm}^3)$.解题关键 本题主要考查了几何体的展开图,利用已知图形得出长方体的长、宽、高是解题关键.

(1)与A相对的面是D;与B相对的面是F;(填大写字母)
(2)悠悠发现A面上的整式为$x^{3}+2x^{2}y + 1$,B面上的整式为$-\frac{1}{2}x^{2}y + x^{3}$,C面上的整式为$\frac{1}{3}x^{2}y - x^{3}$,D面上的整式为$-2(x^{2}y + 1)$,请你计算F面上的整式.
$\frac{1}{2}x^{2}y - 1$

答案：
(1)D F [解析]由正方体表面展开图的“相间、Z 端是对面”可得，“A”与“D”是对面，“B”与“F”是对面，“C”与“E”是对面.
(2)由题意得,$A+D=B+F$,即$(x^{3}+2x^{2}y+1)+[-2(x^{2}y+1)]=(-\frac{1}{2}x^{2}y+x^{3})+F$,所以$F=\frac{1}{2}x^{2}y-1$.

11 中考新考法 操作探究 (2025·广东河源连平期末)综合与探究
[主题]制作无盖长方体盒子.
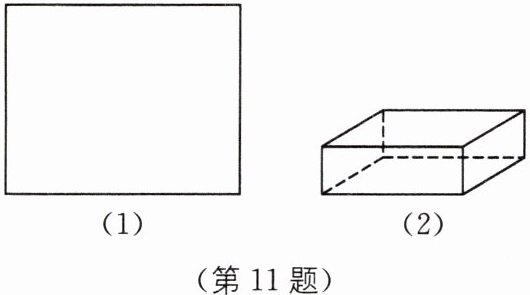
[操作]如图(1)为一块长30cm、宽24cm的长方形纸板,要将其四角各剪去一个正方形,折成如图(2)所示的高为6cm的无盖长方体盒子(纸板厚度忽略不计).
[实践探究]
(1)求折成的无盖长方体盒子的体积;
(2)若用这样的一块长方形纸板折成一个高为4cm的无盖长方体盒子,外表面都涂上色彩,求该盒子需要涂色的面积.

答案：
(1)一块长$30\ \text{cm}$、宽$24\ \text{cm}$的长方形纸板,要将其四角各剪去一个正方形,折成高为$6\ \text{cm}$的无盖长方体盒子,依题意得$(30-6× 2)× (24-6× 2)× 6=18× 12× 6=1296(\text{cm}^3)$,故折成的无盖长方体盒子的体积为$1296\ \text{cm}^3$.
(2)$(30-2× 4)(24-2× 4)+2× 4× (30-2× 4)+2× 4×(24-2× 4)=22× 16+8× 22+8× 16=352+176+128=656(\text{cm}^2)$,故该盒子需要涂色的面积为$656\ \text{cm}^2$.