第105页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
1 (2024·扬州中考)如图是某几何体的表面展开后得到的平面图形,则该几何体是(

A.三棱锥
B.圆锥
C.三棱柱
D.长方体
C
).
A.三棱锥
B.圆锥
C.三棱柱
D.长方体
答案:
C
2 教材P149练习T2·改编 如图所示的正方体,如果把它展开,可以是下列图形中的(


B
).

答案:
B
(1)填空:$a=$
(2)求代数式$5a^{2}b-2(a^{2}b+c)+3(abc-a^{2}b)-4abc$的值.
$-1$
,$b=$$\frac{1}{2}$
,$c=$$\frac{1}{3}$
;(2)求代数式$5a^{2}b-2(a^{2}b+c)+3(abc-a^{2}b)-4abc$的值.
$5a^{2}b-2(a^{2}b+c)+3(abc-a^{2}b)-4abc=5a^{2}b-2a^{2}b-2c+3abc-3a^{2}b-4abc=-2c-abc=-2× (\frac{1}{3})-(-1)×(\frac{1}{2})× (\frac{1}{3})=-\frac{2}{3}+\frac{1}{6}=-\frac{1}{2}$.
答案:
(1)$-1$ $\frac{1}{2}$ $\frac{1}{3}$
(2)$5a^{2}b-2(a^{2}b+c)+3(abc-a^{2}b)-4abc=5a^{2}b-2a^{2}b-2c+3abc-3a^{2}b-4abc=-2c-abc=-2× (\frac{1}{3})-(-1)×(\frac{1}{2})× (\frac{1}{3})=-\frac{2}{3}+\frac{1}{6}=-\frac{1}{2}$.
(1)$-1$ $\frac{1}{2}$ $\frac{1}{3}$
(2)$5a^{2}b-2(a^{2}b+c)+3(abc-a^{2}b)-4abc=5a^{2}b-2a^{2}b-2c+3abc-3a^{2}b-4abc=-2c-abc=-2× (\frac{1}{3})-(-1)×(\frac{1}{2})× (\frac{1}{3})=-\frac{2}{3}+\frac{1}{6}=-\frac{1}{2}$.
4 数学文化 分形 (2024·泰州兴化期末)分形的概念是由数学家本华·曼德博提出的.如图是分形的一种,第1个图案有2个三角形,第2个图案有4个三角形,第3个图案有8个三角形,第4个图案有16个三角形,…,按此规律分形得到第n个图案中三角形的个数是(
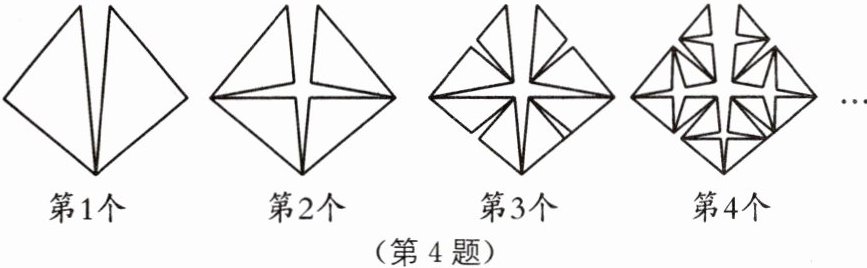
A.$2n$
B.$2^{n - 1}$
C.$2^{n + 1}$
D.$2^{n}$
D
).
A.$2n$
B.$2^{n - 1}$
C.$2^{n + 1}$
D.$2^{n}$
答案:
D
5 教材P148探究·拓展 传统文化 三角垛 我国宋朝时期的数学家杨辉,曾将大小完全相同的圆柱形木桩逐层堆积,形成“三角垛”,顶层记为第1层,有1根圆木桩;前2层有3根圆木桩;前3层有6根圆木桩,往下依次是前4层、前5层…如图,给出了前4层.若用$a_{n}$表示前n层的圆木桩数目,其中$n = 1,2,3,…$,则$\frac{1}{a_{1}}+\frac{1}{a_{2}}+\frac{1}{a_{3}}+…+\frac{1}{a_{16}}$的值是多少?


答案:
观察图形得,$a_{1}=1$,$a_{2}=1+2$,$a_{3}=1+2+3$,$a_{4}=1+2+3+4$,依次类推,$a_{n}=1+2+3+4+\cdots +n=\frac{n(n+1)}{2}$,$\therefore \frac{1}{a_{n}}=\frac{2}{n(n+1)}=2(\frac{1}{n}-\frac{1}{n+1})$.
∵$\frac{1}{a_{1}}=2× (\frac{1}{1}-\frac{1}{2})$,$\frac{1}{a_{2}}=2× (\frac{1}{2}-\frac{1}{3})$,$\frac{1}{a_{3}}=2×(\frac{1}{3}-\frac{1}{4})$,$\cdots$,$\frac{1}{a_{16}}=2× (\frac{1}{16}-\frac{1}{17})$,$\therefore \frac{1}{a_{1}}+\frac{1}{a_{2}}+\frac{1}{a_{3}}+\cdots +\frac{1}{a_{16}}=2× (\frac{1}{1}-\frac{1}{2})+2× (\frac{1}{2}-\frac{1}{3})+2× (\frac{1}{3}-\frac{1}{4})+2×(\frac{1}{16}-\frac{1}{17})=2× (\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\cdots +\frac{1}{16}-\frac{1}{17})=2× (1-\frac{1}{17})=\frac{32}{17}$.
∵$\frac{1}{a_{1}}=2× (\frac{1}{1}-\frac{1}{2})$,$\frac{1}{a_{2}}=2× (\frac{1}{2}-\frac{1}{3})$,$\frac{1}{a_{3}}=2×(\frac{1}{3}-\frac{1}{4})$,$\cdots$,$\frac{1}{a_{16}}=2× (\frac{1}{16}-\frac{1}{17})$,$\therefore \frac{1}{a_{1}}+\frac{1}{a_{2}}+\frac{1}{a_{3}}+\cdots +\frac{1}{a_{16}}=2× (\frac{1}{1}-\frac{1}{2})+2× (\frac{1}{2}-\frac{1}{3})+2× (\frac{1}{3}-\frac{1}{4})+2×(\frac{1}{16}-\frac{1}{17})=2× (\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\cdots +\frac{1}{16}-\frac{1}{17})=2× (1-\frac{1}{17})=\frac{32}{17}$.
查看更多完整答案,请扫码查看


