第75页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
2. 【问题情境】如图,日常生活中,我们经常看到条形码、二维码,他们都是一种编码方式.条形码在一个方向(一般是水平方向)上表述信息,而二维码在水平和竖直两个方向上同时存储信息,相对比下,二维码存储的信息容量要大得多,信息形式更为丰富,它通常使用某种特定的几何图形按一定规律在平面(二维方向)上分布,采用黑白相间的图形记录数据符号信息,所以编码的范围比条形码更广.
【任务学习】在$4×4$的正方形网格中,白色正方形我们用数字0表示,黑色正方形我们用数字1表示.我们把从上往下数叫第i行,从左往右数叫第j列,第i行第j列表示的数我们记为$a(i,j)$(其中i,j都是不大于4的正整数),例如,图①中,$a(1,1)= 0,a(1,2)= 1$,并规定对第i行使用公式$A_{i}= a(i,1)×2^{3}+a(i,2)×2^{2}+a(i,3)×2^{1}+a(i,4)×2^{0}$进行计算($2^{0}= 1$).
【应用生活】某小区为了方便管理,应用上述信息规定为居民设计了一个身份识别图案系统:将图①中所得结果$A_{1},A_{2},A_{3},A_{4}$分别表示居民楼号、单元号、楼层、房间号.如图①中$A_{3}= a(3,1)×2^{3}+a(3,2)×2^{2}+a(3,3)×2^{1}+a(3,4)×2^{0}= 0×8+1×4+0×2+0×1= 4,A_{4}= a(4,1)×2^{3}+a(4,2)×2^{2}+a(4,3)×2^{1}+a(4,4)×2^{0}= 0×8+0×4+1×2+1×1= 3$,说明该居民住在4层,03号房间,即403号.
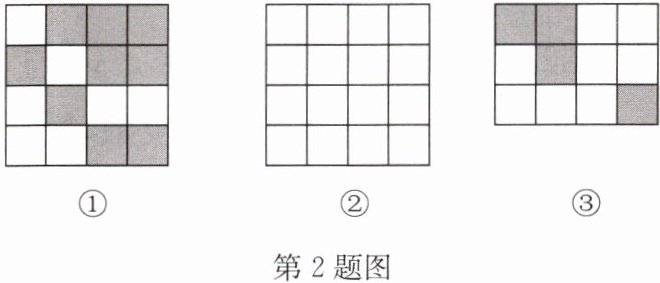
(1)根据题意,王华同学作出了如下的判断:他认为图①代表的居民居住在小区的7号楼10单元,他的判断正确吗?请说明理由;
(2)已知李丽家居住在该小区的5号楼10单元207号,假如你是该小区的网络信息管理员,请你仿照图①,在图②中帮助李丽家设计一张居民的身份识别图案;
(3)图③是该小区某居民的身份识别图案的一部分,由于不小心被损坏看不清第4行了,如果已知该居民居住的房间号不小于7号,则符合该条件的身份识别图案有____张.
【任务学习】在$4×4$的正方形网格中,白色正方形我们用数字0表示,黑色正方形我们用数字1表示.我们把从上往下数叫第i行,从左往右数叫第j列,第i行第j列表示的数我们记为$a(i,j)$(其中i,j都是不大于4的正整数),例如,图①中,$a(1,1)= 0,a(1,2)= 1$,并规定对第i行使用公式$A_{i}= a(i,1)×2^{3}+a(i,2)×2^{2}+a(i,3)×2^{1}+a(i,4)×2^{0}$进行计算($2^{0}= 1$).
【应用生活】某小区为了方便管理,应用上述信息规定为居民设计了一个身份识别图案系统:将图①中所得结果$A_{1},A_{2},A_{3},A_{4}$分别表示居民楼号、单元号、楼层、房间号.如图①中$A_{3}= a(3,1)×2^{3}+a(3,2)×2^{2}+a(3,3)×2^{1}+a(3,4)×2^{0}= 0×8+1×4+0×2+0×1= 4,A_{4}= a(4,1)×2^{3}+a(4,2)×2^{2}+a(4,3)×2^{1}+a(4,4)×2^{0}= 0×8+0×4+1×2+1×1= 3$,说明该居民住在4层,03号房间,即403号.

(1)根据题意,王华同学作出了如下的判断:他认为图①代表的居民居住在小区的7号楼10单元,他的判断正确吗?请说明理由;
(2)已知李丽家居住在该小区的5号楼10单元207号,假如你是该小区的网络信息管理员,请你仿照图①,在图②中帮助李丽家设计一张居民的身份识别图案;
(3)图③是该小区某居民的身份识别图案的一部分,由于不小心被损坏看不清第4行了,如果已知该居民居住的房间号不小于7号,则符合该条件的身份识别图案有____张.
答案:
(1)解:不正确.理由:由题意得A₁=a(1,1)×2³+a(1,2)×2²+a(1,3)×2¹+a(1,4)×2⁰=0×8+1×4+1×2+1×1=7,A₂=a(2,1)×2³+a(2,2)×2²+a(2,3)×2¹+a(2,4)×2⁰=1×8+0×4+1×2+1×1=11,则图①代表的居民居住在小区的7号楼11单元.即王华的判断不正确.
(2)解:如答图所示.
(3)9
(1)解:不正确.理由:由题意得A₁=a(1,1)×2³+a(1,2)×2²+a(1,3)×2¹+a(1,4)×2⁰=0×8+1×4+1×2+1×1=7,A₂=a(2,1)×2³+a(2,2)×2²+a(2,3)×2¹+a(2,4)×2⁰=1×8+0×4+1×2+1×1=11,则图①代表的居民居住在小区的7号楼11单元.即王华的判断不正确.
(2)解:如答图所示.

(3)9
查看更多完整答案,请扫码查看


