第114页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
1. 十八世纪瑞士数学家欧拉证明了简单多面体的顶点数$(V)$、面数$(F)$、棱数$(E)$之间存在的一个有趣的关系式,被称为欧拉公式. 请你观察下列如图①所示的五种简单多面体模型,解答下列问题:
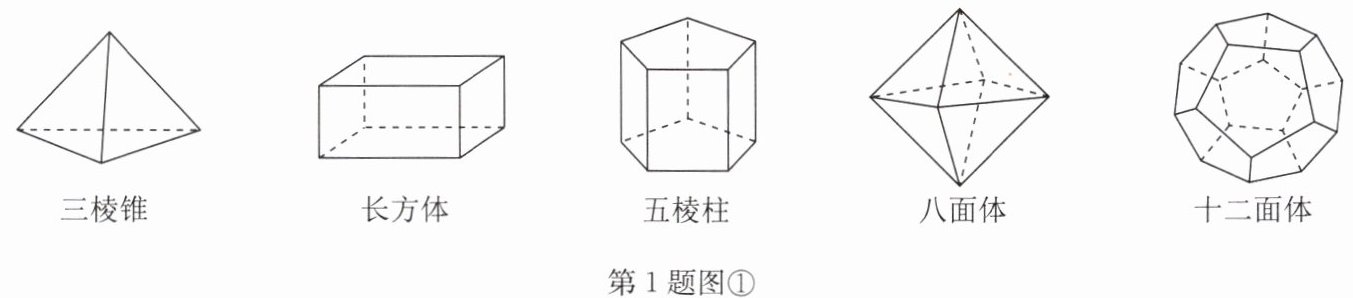
【观察总结】(1)五种简单多面体的顶点数$(V)$、面数$(F)$、棱数$(E)$如下表:
|多面体|顶点数$(V)$|面数$(F)$|棱数$(E)$|
|三棱锥|4|4|6|
|长方体|8|6|12|
|五棱柱|10|7|15|
|八面体|6|8|12|
|十二面体|20|12|30|
猜想顶点数$(V)$、面数$(F)$、棱数$(E)$之间存在的关系式是
【简单应用】(2)能否组成一个有24条棱、10个面、13个顶点的多面体?请说明理由.
(3)一个正二十面体有30条棱,则它的顶点数是
【实践探究】(4)学校校园文化节,七年级数学实践小组同学制作了各种各样的多面体作品.
①一个多面体作品,只有12个顶点,并且过每个顶点都有4条棱,则这个多面体的面数是
②一个多面体作品如图②所示,每个面的形状是正三角形或正五边形,每条棱都是正三角形和正五边形的公共边,则该多面体作品正三角形比正五边形的面数多


【观察总结】(1)五种简单多面体的顶点数$(V)$、面数$(F)$、棱数$(E)$如下表:
|多面体|顶点数$(V)$|面数$(F)$|棱数$(E)$|
|三棱锥|4|4|6|
|长方体|8|6|12|
|五棱柱|10|7|15|
|八面体|6|8|12|
|十二面体|20|12|30|
猜想顶点数$(V)$、面数$(F)$、棱数$(E)$之间存在的关系式是
V+F−E=2
. (用所给的字母表达)【简单应用】(2)能否组成一个有24条棱、10个面、13个顶点的多面体?请说明理由.
解:不能,理由:因为10+13−24=−1≠2,所以不能组成一个有24条棱、10个面、13个顶点的多面体.
(3)一个正二十面体有30条棱,则它的顶点数是
12
.【实践探究】(4)学校校园文化节,七年级数学实践小组同学制作了各种各样的多面体作品.
①一个多面体作品,只有12个顶点,并且过每个顶点都有4条棱,则这个多面体的面数是
14
;②一个多面体作品如图②所示,每个面的形状是正三角形或正五边形,每条棱都是正三角形和正五边形的公共边,则该多面体作品正三角形比正五边形的面数多
8
个.
答案:
(1)V+F−E=2
(2)解:不能,理由:
因为10+13−24=−1≠2,
所以不能组成一个有24条棱、10个面、13个顶点的多面体.
(3)12
(4)①14 ②8
(1)V+F−E=2
(2)解:不能,理由:
因为10+13−24=−1≠2,
所以不能组成一个有24条棱、10个面、13个顶点的多面体.
(3)12
(4)①14 ②8
查看更多完整答案,请扫码查看


