第95页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
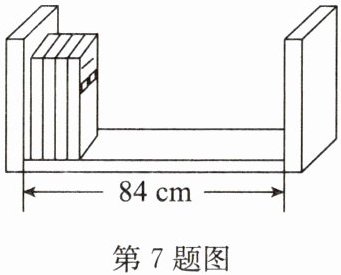
7. (2024·江西改编)如图,书架宽84 cm,在该书架上按图示方式摆放数学书和语文书,已知每本数学书厚0.8 cm,每本语文书厚1.2 cm.
(1)数学书和语文书共90本恰好摆满该书架,求书架上摆了数学书和语文书各多少本;
(2)如果书架上已摆放了10本语文书,那么数学书最多还可以摆放多少本?
(1)数学书和语文书共90本恰好摆满该书架,求书架上摆了数学书和语文书各多少本;
(2)如果书架上已摆放了10本语文书,那么数学书最多还可以摆放多少本?

答案:
(1)设书架上摆了数学书x本,语文书(90-x)本,
根据题意,得0.8x+1.2(90-x)=84,解得x=60,
所以90-x=30.
答:书架上摆了数学书60本,语文书30本.
(2)84-1.2×10=72(cm),
72÷0.8=90(本)
答:数学书最多还可以摆放90本.
(1)设书架上摆了数学书x本,语文书(90-x)本,
根据题意,得0.8x+1.2(90-x)=84,解得x=60,
所以90-x=30.
答:书架上摆了数学书60本,语文书30本.
(2)84-1.2×10=72(cm),
72÷0.8=90(本)
答:数学书最多还可以摆放90本.
8. 生活中处处有数学,如图,表一是某月的日历表,用一个长方形框出了9个数.
(1)若一个长方形框内9个数字之和是108,求出它中间的数字;
(2)将自然数1至2024按表二的方式排列,框出9个数其和能为2025吗?若能,求出该长方形框中的最小数;若不能,请说明理由.

(1)若一个长方形框内9个数字之和是108,求出它中间的数字;
(2)将自然数1至2024按表二的方式排列,框出9个数其和能为2025吗?若能,求出该长方形框中的最小数;若不能,请说明理由.

答案:
(1)设中间的数字为a,则9a=108,解得a=12.
(2)不能.理由:设长方形框的中间数字为x,
根据题意,得9x=2025,解得x=225.
因为225÷7=32……1,所以225在第1列,
故这样的9个数不存在.
(1)设中间的数字为a,则9a=108,解得a=12.
(2)不能.理由:设长方形框的中间数字为x,
根据题意,得9x=2025,解得x=225.
因为225÷7=32……1,所以225在第1列,
故这样的9个数不存在.
9. 用同样规格的灰白两种颜色的正方形瓷砖,按如图的方式铺地面.
(1)观察图形,填写下表:
|图形|①|②|③|…|
|灰色瓷砖的块数|4|7|
|灰白两种瓷砖的总块数|9|15|
(2)依上表可推测,第$n$个图形中灰色瓷砖的数量为
(3)白色瓷砖与灰色瓷砖的总数量可能是2024块吗?若能,求出是第几个图形;若不能,请说明理由.
(1)观察图形,填写下表:
|图形|①|②|③|…|
|灰色瓷砖的块数|4|7|
10
|…||灰白两种瓷砖的总块数|9|15|
21
|…|(2)依上表可推测,第$n$个图形中灰色瓷砖的数量为
(3n+1)
块,灰白两种瓷砖的总数量为(6n+3)
块;(用含$n$的代数式表示)(3)白色瓷砖与灰色瓷砖的总数量可能是2024块吗?若能,求出是第几个图形;若不能,请说明理由.
解:不能.理由如下:
令6n+3=2024,解得$n=336\frac{5}{6},$又因为n为正整数,所以白色瓷砖与灰色瓷砖的总数量不能是2024块.
令6n+3=2024,解得$n=336\frac{5}{6},$又因为n为正整数,所以白色瓷砖与灰色瓷砖的总数量不能是2024块.
答案:
(1)10 21
(2)(3n+1) (6n+3)
(3)解:不能.理由如下:
令6n+3=2024,解得$n=336\frac{5}{6},$又因为n为正整数,所以白色瓷砖与灰色瓷砖的总数量不能是2024块.
(1)10 21
(2)(3n+1) (6n+3)
(3)解:不能.理由如下:
令6n+3=2024,解得$n=336\frac{5}{6},$又因为n为正整数,所以白色瓷砖与灰色瓷砖的总数量不能是2024块.
查看更多完整答案,请扫码查看


