1. 在数轴上,$ O $ 为原点,点 $ M $ 对应的数为 $ 10 $,点 $ N $ 对应的数为 $ -2 $. 若点 $ P $ 从点 $ N $ 出发以 $ 1 $ 个单位长度/秒的速度沿数轴正方向运动,点 $ Q $ 从点 $ M $ 出发以 $ 2 $ 个单位长度/秒的速度沿数轴负方向运动,经过
3 或 5
秒,$ P,Q $ 两点相距 $ 3 $ 个单位长度.
答案:
3 或 5
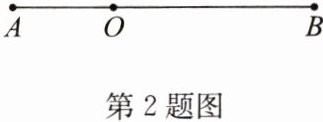
2. 如图,线段 $ AB = 24\mathrm{cm} $,$ O $ 为线段 $ AB $ 上一点,且 $ OA:OB = 1:2 $. 动点 $ P $ 以 $ 1\mathrm{cm}/\mathrm{s} $ 的速度,从点 $ O $ 出发,沿 $ OB $ 方向运动,运动到点 $ B $ 停止;点 $ P $ 出发 $ 1\mathrm{s} $ 后,点 $ Q $ 以 $ 4\mathrm{cm}/\mathrm{s} $ 的速度,从点 $ O $ 出发,沿 $ OA $ 方向运动,运动到点 $ A $ 时,停留 $ 2\mathrm{s} $,然后按原速沿 $ AB $ 方向运动到点 $ B $ 停止. 设点 $ P $ 的运动时间为 $ t\mathrm{s} $.
(1)$ OA = $
(2)当点 $ Q $ 从点 $ O $ 向点 $ A $ 运动时,若 $ OQ = 2OP $,求 $ t $ 的值.
(3)当 $ PQ = 2\mathrm{cm} $ 时,求 $ t $ 的值.
(1)$ OA = $
8
$\mathrm{cm} $,$ OB = $16
$\mathrm{cm} $;(2)当点 $ Q $ 从点 $ O $ 向点 $ A $ 运动时,若 $ OQ = 2OP $,求 $ t $ 的值.
解:当点 Q 从点 O 向点 A 运动时,OP=t cm,OQ=4(t-1)=(4t-4)cm,因为 OQ=2OP,所以 4t-4=2t,解得 t=2,即 t 的值为 2.
(3)当 $ PQ = 2\mathrm{cm} $ 时,求 $ t $ 的值.
解:当点 Q 追上点 P 时,可得 4(t-5)=8+t,解得$t=\frac{28}{3}$.
①当1≤t≤3时,即点 Q 向点 A 运动,则 4(t-1)+t=2,解得$t=\frac{6}{5}$.
②当$5\leq t\leq \frac{28}{3}$时,即点 Q 从点 A 向点 B 运动,且点 Q 在点 P 的左侧,则 4(t-5)+2=8+t,解得$t=\frac{26}{3}$.
③当$\frac{28}{3}<t\leq11$时,即点 Q 从点 A 向点 B 运动,且点 Q 在点 P 的右侧,则 4(t-5)-2=8+t,解得 t=10.
④当11<t≤16时,即点 Q 到达点 B 后停止运动,点 P 继续从点 O 向点 B 运动,则 t+2=16,解得 t=14.
综上,当 PQ=2 cm 时,t 的值为$\frac{6}{5}$或$\frac{26}{3}$或 10 或 14.
①当1≤t≤3时,即点 Q 向点 A 运动,则 4(t-1)+t=2,解得$t=\frac{6}{5}$.
②当$5\leq t\leq \frac{28}{3}$时,即点 Q 从点 A 向点 B 运动,且点 Q 在点 P 的左侧,则 4(t-5)+2=8+t,解得$t=\frac{26}{3}$.
③当$\frac{28}{3}<t\leq11$时,即点 Q 从点 A 向点 B 运动,且点 Q 在点 P 的右侧,则 4(t-5)-2=8+t,解得 t=10.
④当11<t≤16时,即点 Q 到达点 B 后停止运动,点 P 继续从点 O 向点 B 运动,则 t+2=16,解得 t=14.
综上,当 PQ=2 cm 时,t 的值为$\frac{6}{5}$或$\frac{26}{3}$或 10 或 14.

答案:
(1)8 16
(2)解:当点 Q 从点 O 向点 A 运动时,OP=t cm,OQ=4(t-1)=(4t-4)cm,因为 OQ=2OP,所以 4t-4=2t,解得 t=2,即 t 的值为 2.
(3)解:当点 Q 追上点 P 时,可得 4(t-5)=8+t,解得$t=\frac{28}{3}$.
①当1≤t≤3时,即点 Q 向点 A 运动,则 4(t-1)+t=2,解得$t=\frac{6}{5}$.
②当$5\leq t\leq \frac{28}{3}$时,即点 Q 从点 A 向点 B 运动,且点 Q 在点 P 的左侧,则 4(t-5)+2=8+t,解得$t=\frac{26}{3}$.
③当$\frac{28}{3}<t\leq11$时,即点 Q 从点 A 向点 B 运动,且点 Q 在点 P 的右侧,则 4(t-5)-2=8+t,解得 t=10.
④当11<t≤16时,即点 Q 到达点 B 后停止运动,点 P 继续从点 O 向点 B 运动,则 t+2=16,解得 t=14.
综上,当 PQ=2 cm 时,t 的值为$\frac{6}{5}$或$\frac{26}{3}$或 10 或 14.
(1)8 16
(2)解:当点 Q 从点 O 向点 A 运动时,OP=t cm,OQ=4(t-1)=(4t-4)cm,因为 OQ=2OP,所以 4t-4=2t,解得 t=2,即 t 的值为 2.
(3)解:当点 Q 追上点 P 时,可得 4(t-5)=8+t,解得$t=\frac{28}{3}$.
①当1≤t≤3时,即点 Q 向点 A 运动,则 4(t-1)+t=2,解得$t=\frac{6}{5}$.
②当$5\leq t\leq \frac{28}{3}$时,即点 Q 从点 A 向点 B 运动,且点 Q 在点 P 的左侧,则 4(t-5)+2=8+t,解得$t=\frac{26}{3}$.
③当$\frac{28}{3}<t\leq11$时,即点 Q 从点 A 向点 B 运动,且点 Q 在点 P 的右侧,则 4(t-5)-2=8+t,解得 t=10.
④当11<t≤16时,即点 Q 到达点 B 后停止运动,点 P 继续从点 O 向点 B 运动,则 t+2=16,解得 t=14.
综上,当 PQ=2 cm 时,t 的值为$\frac{6}{5}$或$\frac{26}{3}$或 10 或 14.
3. 在数轴上有 $ A,B $ 两点,它们表示的数分别为 $ a,b $.
(1)如图①,如果点 $ C,D $ 在线段 $ AB $ 上,且 $ AC = BD $,猜想 $ AD $ 与 $ BC $ 有怎样的数量关系,并说明理由.
(2)如图②,点 $ P $ 由点 $ B $ 沿着数轴先向左移动 $ (2b - 2a + 1) $ 个单位长度,再向右移动 $ \left( \frac { 3 } { 2 } b - \frac { 3 } { 2 } a + 1 \right) $ 个单位长度得到.
①如果 $ a = - 4,b = 6 $ 时,那么点 $ P $ 表示的数为
②对任意 $ a,b $ 的值,试说明 $ P $ 是线段 $ AB $ 的中点.
(1)如图①,如果点 $ C,D $ 在线段 $ AB $ 上,且 $ AC = BD $,猜想 $ AD $ 与 $ BC $ 有怎样的数量关系,并说明理由.
(1)解:AD=BC.理由如下:因为 AD=AC+CD,BC=BD+CD,又因为 AC=BD,所以 AD=BC.
(2)如图②,点 $ P $ 由点 $ B $ 沿着数轴先向左移动 $ (2b - 2a + 1) $ 个单位长度,再向右移动 $ \left( \frac { 3 } { 2 } b - \frac { 3 } { 2 } a + 1 \right) $ 个单位长度得到.
①如果 $ a = - 4,b = 6 $ 时,那么点 $ P $ 表示的数为
1
;②对任意 $ a,b $ 的值,试说明 $ P $ 是线段 $ AB $ 的中点.
(2)②解:因为点 P 由点 B 沿着数轴先向左移动(2b-2a+1)个单位长度,再向右移动$(\frac{3}{2}b-\frac{3}{2}a+1)$个单位长度得到,所以点 P 表示的数是$b-(2b-2a+1)+\frac{3}{2}b-\frac{3}{2}a+1=\frac{1}{2}(a+b)$.因为线段 AB 的中点表示的数为$\frac{1}{2}(a+b)$,所以 P 是线段 AB 的中点.
答案:
(1)解:AD=BC.理由如下:因为 AD=AC+CD,BC=BD+CD,又因为 AC=BD,所以 AD=BC.
(2)①1
②解:因为点 P 由点 B 沿着数轴先向左移动(2b-2a+1)个单位长度,再向右移动$(\frac{3}{2}b-\frac{3}{2}a+1)$个单位长度得到,所以点 P 表示的数是$b-(2b-2a+1)+\frac{3}{2}b-\frac{3}{2}a+1=\frac{1}{2}(a+b)$.因为线段 AB 的中点表示的数为$\frac{1}{2}(a+b)$,所以 P 是线段 AB 的中点.
(1)解:AD=BC.理由如下:因为 AD=AC+CD,BC=BD+CD,又因为 AC=BD,所以 AD=BC.
(2)①1
②解:因为点 P 由点 B 沿着数轴先向左移动(2b-2a+1)个单位长度,再向右移动$(\frac{3}{2}b-\frac{3}{2}a+1)$个单位长度得到,所以点 P 表示的数是$b-(2b-2a+1)+\frac{3}{2}b-\frac{3}{2}a+1=\frac{1}{2}(a+b)$.因为线段 AB 的中点表示的数为$\frac{1}{2}(a+b)$,所以 P 是线段 AB 的中点.
查看更多完整答案,请扫码查看


