1. 解方程:(1)$\frac {0.4x+0.9}{0.5}-\frac {0.03+0.02x}{0.03}= \frac {x-5}{2}$;(2)$\frac {3}{4}[\frac {4}{3}(\frac {1}{4}x-1)+8]= \frac {7}{3}+\frac {2}{3}x$。
答案:
1.解:
(1)整理,得$\frac{4x+9}{5}-\frac{3+2x}{3}=\frac{x-5}{2}$,
去分母,得$6(4x+9)-10(3+2x)=15(x-5)$,
去括号,得$24x+54-30-20x=15x-75$,
移项,得$24x-20x-15x=-75-54+30$,
合并同类项,得$-11x=-99$,系数化为1,得$x=9$.
(2)去括号,得$\frac{1}{4}x-1+6=\frac{7}{3}+\frac{2}{3}x$,
去分母,得$3x-12+72=28+8x$,
移项、合并同类项,得$-5x=-32$,系数化为1,得$x=\frac{32}{5}$.
(1)整理,得$\frac{4x+9}{5}-\frac{3+2x}{3}=\frac{x-5}{2}$,
去分母,得$6(4x+9)-10(3+2x)=15(x-5)$,
去括号,得$24x+54-30-20x=15x-75$,
移项,得$24x-20x-15x=-75-54+30$,
合并同类项,得$-11x=-99$,系数化为1,得$x=9$.
(2)去括号,得$\frac{1}{4}x-1+6=\frac{7}{3}+\frac{2}{3}x$,
去分母,得$3x-12+72=28+8x$,
移项、合并同类项,得$-5x=-32$,系数化为1,得$x=\frac{32}{5}$.
2. 解方程:$\frac {x}{1×2}+\frac {x}{2×3}+\frac {x}{3×4}+... +\frac {x}{2023×2024}= 2023$。
答案:
2.解:原方程可变形为
$(\frac{1}{1×2}+\frac{1}{2×3}+\frac{1}{3×4}+…+\frac{1}{2023×2024})x=2023$,
即$(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+…+\frac{1}{2022}-\frac{1}{2023}+\frac{1}{2023}-$
$\frac{1}{2024})x=2023$,
$(1-\frac{1}{2024})x=2023$,$\frac{2023}{2024}x=2023$,解得$x=2024$.
$(\frac{1}{1×2}+\frac{1}{2×3}+\frac{1}{3×4}+…+\frac{1}{2023×2024})x=2023$,
即$(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+…+\frac{1}{2022}-\frac{1}{2023}+\frac{1}{2023}-$
$\frac{1}{2024})x=2023$,
$(1-\frac{1}{2024})x=2023$,$\frac{2023}{2024}x=2023$,解得$x=2024$.
3. 若a,b,c,d是正数,解方程: $\frac {x-a-b-c}{d}+\frac {x-a-b-d}{c}+\frac {x-a-c-d}{b}+\frac {x-b-c-d}{a}= 4$。
$\frac {x-a-b-c}{d}+\frac {x-a-b-d}{c}+\frac {x-a-c-d}{b}+\frac {x-b-c-d}{a}= 4$。
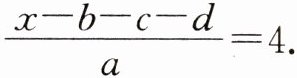
 $\frac {x-a-b-c}{d}+\frac {x-a-b-d}{c}+\frac {x-a-c-d}{b}+\frac {x-b-c-d}{a}= 4$。
$\frac {x-a-b-c}{d}+\frac {x-a-b-d}{c}+\frac {x-a-c-d}{b}+\frac {x-b-c-d}{a}= 4$。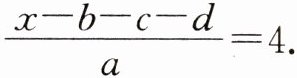
答案:
3.解:方程变形为$\frac{x-a-b-c}{d}-1+\frac{x-a-b-d}{c}-1+$
$\frac{x-a-c-d}{b}-1+\frac{x-b-c-d}{a}-1=0$,整理,得
$\frac{x-a-b-c-d}{d}+\frac{x-a-b-c-d}{c}+\frac{x-a-b-c-d}{b}+$
$\frac{x-a-b-c-d}{a}=0$,
$(x-a-b-c-d)(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d})=0$.
因为a,b,c,d是正数,所以$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}≠0$,
所以$x-a-b-c-d=0$,所以$x=a+b+c+d$.
$\frac{x-a-c-d}{b}-1+\frac{x-b-c-d}{a}-1=0$,整理,得
$\frac{x-a-b-c-d}{d}+\frac{x-a-b-c-d}{c}+\frac{x-a-b-c-d}{b}+$
$\frac{x-a-b-c-d}{a}=0$,
$(x-a-b-c-d)(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d})=0$.
因为a,b,c,d是正数,所以$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{d}≠0$,
所以$x-a-b-c-d=0$,所以$x=a+b+c+d$.
查看更多完整答案,请扫码查看


