《2025年启东中学作业本七年级数学上册苏科版盐城专版》

1. 已知有理数 $a,b,c$ 对应的点在数轴上的位置如图所示,且 $|b|＞|c|$,化简 $2|c - b|-|a + c|= $ 3c-2b+a.

答案： 3c-2b+a 点拨:由题图可知,a＜b＜0＜c. 因为|b|＞|c|,所以|a|＞|c|, 所以 c-b＞0,a+c＜0, 所以 2|c-b|-|a+c|=2(c-b)-[-(a+c)]=2c-2b+ a+c=3c-2b+a.

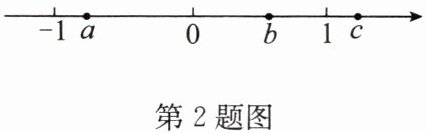
2. 已知有理数 $a,b,c$ 对应的点在数轴上的位置如图所示.
化简：$|2a - b|+2|c - b|-3|a + c|$.

答案： 解:由数轴知-1＜a＜0＜b＜1＜c,且|b|＜|a|＜|c|, 则 2a-b＜0,c-b＞0,a+c＞0, 所以原式=-(2a-b)+2(c-b)-3(a+c) =-2a+b+2c-2b-3a-3c =-5a-b-c.

3. 阅读下列材料并解决有关问题.
化简代数式 $|m + 1|+|m - 2|$.
解：令 $m + 1 = 0$ 和 $m - 2 = 0$,分别求得 $m = -1,m = 2$(称 $-1,2$ 分别为 $|m + 1|$ 与 $|m - 2|$ 的零点值). 在有理数范围内,零点值 $m = -1$ 和 $m = 2$ 可将全体有理数分成不重复且不遗漏的 3 种情况：① $m ＜ -1$；② $-1\leqslant m ＜ 2$；③ $m\geqslant 2$.
从而化简代数式 $|m + 1|+|m - 2|$ 可分以下 3 种情况：
①当 $m ＜ -1$ 时,原式 $=-(m + 1)-(m - 2)= -2m + 1$；
②当 $-1\leqslant m ＜ 2$ 时,原式 $=m + 1-(m - 2)= 3$；
③当 $m\geqslant 2$ 时,原式 $=m + 1 + m - 2 = 2m - 1$.
综上,原式 $=\begin{cases}-2m + 1(m ＜ -1),\\3(-1\leqslant m ＜ 2),\\2m - 1(m\geqslant 2).\end{cases} $
通过以上阅读,请你解决下列问题：
(1)求 $|x - 5|$ 和 $|x - 4|$ 的零点值；
(2)化简代数式 $|x - 5|+|x - 4|$；
(3)求代数式 $|x - 5|+|x - 4|$ 的最小值.

答案： 解:
(1)令x-5=0,x-4=0, 解得x=5和x=4, 故|x-5|和|x-4|的零点值分别为5和4.
(2)当x＜4时,原式=5-x+4-x=9-2x. 当4≤x＜5时,原式=5-x+x-4=1. 当x≥5时,原式=x-5+x-4=2x-9. 综上,原式= {9-2x(x＜4), 1(4≤x＜5), 2x-9(x≥5).
(3)当x＜4时,原式=9-2x＞1. 当4≤x＜5时,原式=1. 当x≥5时,原式=2x-9≥1. 故代数式的最小值是1.