《2025年启东中学作业本七年级数学上册苏科版盐城专版》

1. 任意大于 1 的正整数 $ n $ 的三次幂均可“分裂”成 $ n $ 个连续奇数的和. 例如,$ 2^{3}= 3 + 5 $,$ 3^{3}= 7 + 9 + 11 $,$ 4^{3}= 13 + 15 + 17 + 19 $,…$$. 若 $ m^{3} $ 的“分裂数”中有一个是 119,则 $ m = $(B)
A.10
B.11
C.12
D.13

答案： B 点拨:因为 $2^{3}=3+5,3^{3}=7+9+11,4^{3}=13+15+17+19,\cdots$,所以 $n^{3}$ 分裂后的第一个数是 $n(n-1)+1$,共有 $n$ 个奇数.因为 $11×(11-1)+1=111,12×(12-1)+1=133$,所以奇数 119 是 $11^{3}$ 分裂后的一个奇数，所以 $m=11$.

2. 1 根 1 米长的木棒,第一次截去一半,第二次截去剩下的一半……如此截下去,则第 2024 次剩下的木棒的长为$\left(\frac{1}{2}\right)^{2024}$米.

答案： $\left(\frac{1}{2}\right)^{2024}$

3. 若规定 $ f(n) $ 为 $ 2^{n} $ 的个位数字,例如,$ 2^{1}= 2 $,所以 $ f(1)= 2 $；$ 2^{4}= 16 $,所以 $ f(4)= 6 $. 计算 $ f(1)+f(2)+f(3)+f(4)+… +f(2024)= $10120.

答案： 10120 点拨:因为 $f(1)=2,f(2)=4,f(3)=8,f(4)=6$,$f(5)=2,f(6)=4,\cdots$,所以这列数以 2,4,8,6 为一个循环,依次出现.而 $2024=4×506$,所以 $f(2024)=6$,所以 $f(1)+f(2)+f(3)+f(4)+\cdots+f(2024)=(2+4+8+6)×506=20×506=10120$.

1. 有一个数字游戏,第一步：取一个自然数 $ n_{1}= 4 $,计算 $ n_{1} \cdot (3n_{1}+1) $ 得 $ a_{1} $；第二步：算出 $ a_{1} $ 的各位数字之和 $ n_{2} $,计算 $ n_{2} \cdot (3n_{2}+1) $ 得 $ a_{2} $；第三步：算出 $ a_{2} $ 的各位数字之和 $ n_{3} $,计算 $ n_{3} \cdot (3n_{3}+1) $ 得 $ a_{3} … … $ 依此类推,则 $ a_{2024} $ 的值为(C)
A.7
B.52
C.154
D.310

答案： C 点拨:由题意可得，n₁=4,a₁=4×(3×4+1)=52,n₂=5+2=7,a₂=7×(3×7+1)=154,n₃=1+5+4=10,a₃=10×(3×10+1)=310,n₄=3+1+0=4,a₄=4×(3×4+1)=52,……所以这列数以 52,154,310 为一个循环,依次出现.因为 2024÷3=674……2,所以 a₂₀₂₄的值为 154.

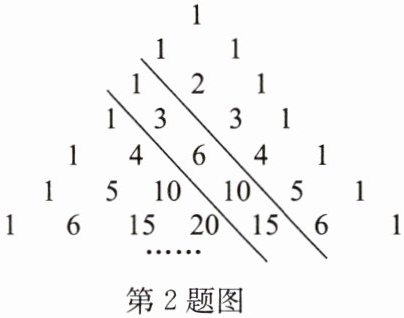
2. 如图被称为“杨辉三角”. 图中两平行线之间的一列数：1,3,6,10,15,…,我们把第一个数记为 $ a_{1} $,第二个数记为 $ a_{2} $,第三个数记为 $ a_{3} $,…,第 $ n $ 个数记为 $ a_{n} $,则 $ a_{4}+a_{200}= $______20110.

答案： 20110 点拨:根据题意知 a₁=1,a₂=1+2=3,a₃=1+2+3=6,a₄=1+2+3+4=10,…,则 aₙ=1+2+3+…+n=$\frac{1}{2}$n(n+1),所以 a₄+a₂₀₀=10+$\frac{1}{2}$×200×(200+1)=10+20100=20110.

3. 现有一列整数,第一个数为 1,第二个数为 $ x $($ x $ 为正整数). 以后每一个数都由它前一个数与再前一个数的差的绝对值得到. 如第三个数由 $ x $ 与 1 的差的绝对值得到,即为 $ |x - 1| $,第四个数由 $ |x - 1| $ 与 $ x $ 的差的绝对值得到,即为 $ ||x - 1| - x| … … $ 依此类推. 要使这列数的前 100 个数中恰好有 30 个 0,则 $ x = $______6 或 7.

答案： 6 或 7 点拨:①x 为正偶数时,这列数为 1,x,|x-1|,1,|x-2|,|x-3|,…,1,2,1,1,0,1,1,0,1,…,观察可得出，每 3 个数为一组,每组第 1 个数均为 1,第 2 个,第 3 个数从 x 开始依次减 1,直至减到 1,然后开始 1,0,1 循环.因为前 100 个数中恰好有 30 个 0,所以 100÷3=33……1,则前 3 组不含 0,即前 3 组的第 2 个,第 3 个数从 x 开始减到 1,从第 4 组开始后 30 组均为 1,0,1,所以 2×3=6,则 x=6.②x 为正奇数时,这列数为 1,x,|x-1|,1,|x-2|,|x-3|,…,1,3,2,1,1,0,1,1,0,…,观察可得出,每 3 个数为一组,每组第 1 个数均为 1,第 2 个,第 3 个数从 x 开始依次减 1,直至减到 2,然后开始 1,1,0 循环.因为前 100 个数中恰好有 30 个 0,所以 100÷3=33……1,则前 3 组不含 0,即前 3 组的第 2 个,第 3 个数从 x 开始减到 2,从第 4 组开始后 30 组均为 1,1,0,所以 2×3=6,则 x=6+1=7.综上所述,x 的值为 6 或 7.