《2025年中学生世界六年级数学上册沪教版五四制》

19. 若一个角等于这个角的补角的$\frac{1}{8}$,求这个角的度数.

答案： 解：设这个角的度数为$x$，则它的补角的度数为$180^{\circ}-x$。
根据题意，得$x=\frac{1}{8}(180^{\circ}-x)$。
方程两边同时乘以8，得$8x=180^{\circ}-x$。
移项，得$8x+x=180^{\circ}$。
合并同类项，得$9x=180^{\circ}$。
系数化为1，得$x=20^{\circ}$。
答：这个角的度数为$20^{\circ}$。

20. 已知$\angle 1和\angle 2$互为余角,$\angle 1比\angle 2大40^\circ$.求$4\angle 2-\frac{1}{5}\angle 1$的度数.

答案： 解：因为∠1和∠2互为余角，所以∠1+∠2=90°。
又因为∠1比∠2大40°，所以∠1=∠2+40°。
将∠1=∠2+40°代入∠1+∠2=90°，得∠2+40°+∠2=90°，
2∠2=50°，∠2=25°。
则∠1=25°+40°=65°。
所以4∠2-1/5∠1=4×25°-1/5×65°=100°-13°=87°。
答：4∠2-1/5∠1的度数为87°。

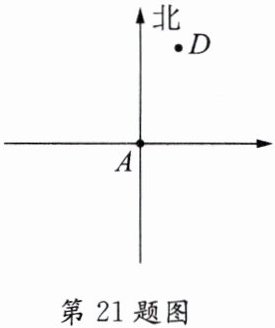
21. 如图,已知点A表示A城,点D表示D城.
(1)如果B城在A城的南偏东$60^\circ$方向,请画出从A城到B城方向的射线；
(2)如果C城在A城的北偏西$30^\circ$方向,在D城的南偏西$60^\circ$方向,请确定C城的位置(用点C表示).
要求:不写画法,保留画图痕迹,写出结论.

答案：

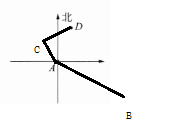
结论：
(1) 以点$A$为原点，向南偏东$60^\circ$方向画射线，该射线即为$A$城到$B$城的方向。
(2) 以点$A$为原点，向北偏西$30^\circ$方向画射线$l_1$；再以点$D$为原点，向南偏西$60^\circ$方向画射线$l_2$，两条射线的交点即为点$C$的位置。

22. 已知在任何一个三角形中,三个内角的和等于$180^\circ$.现有三角形ABC,BO和CO分别是$\angle ABC与\angle ACB$的平分线,如果$\angle A= 50^\circ$,试求$\angle BOC$的大小.

答案： 解析：本题可根据三角形内角和定理以及角平分线的性质来求解$\angle BOC$的度数。
1. 首先，在$\triangle ABC$中，已知$\angle A = 50^{\circ}$，根据三角形内角和为$180^{\circ}$，可得$\angle ABC + \angle ACB = 180^{\circ} - \angle A = 180^{\circ} - 50^{\circ} = 130^{\circ}$。
2. 因为$BO$和$CO$分别是$\angle ABC$与$\angle ACB$的平分线，所以$\angle OBC=\frac{1}{2}\angle ABC$，$\angle OCB=\frac{1}{2}\angle ACB$。
3. 那么$\angle OBC + \angle OCB = \frac{1}{2}(\angle ABC + \angle ACB)=\frac{1}{2}×130^{\circ} = 65^{\circ}$。
4. 最后，在$\triangle BOC$中，根据三角形内角和为$180^{\circ}$，可得$\angle BOC = 180^{\circ} - (\angle OBC + \angle OCB)=180^{\circ} - 65^{\circ} = 115^{\circ}$。
答案：$\angle BOC = 115^{\circ}$。