1. 已知∠AOB= 78°,∠AOC= 42°,OC在∠AOB内部,则∠BOC的度数为 (
A.120°;
B.42°;
C.36°;
D.不确定.
C
)A.120°;
B.42°;
C.36°;
D.不确定.
答案:
解析:
本题主要考查角的和、差计算。
已知$\angle AOB = 78^\circ$,$\angle AOC = 42^\circ$,且$OC$在$\angle AOB$内部。
根据角的和、差关系,有:
$\angle BOC = \angle AOB - \angle AOC$。
将已知的角度值代入上式,得:
$\angle BOC = 78^\circ - 42^\circ = 36^\circ$。
答案:C.$36^\circ$。
本题主要考查角的和、差计算。
已知$\angle AOB = 78^\circ$,$\angle AOC = 42^\circ$,且$OC$在$\angle AOB$内部。
根据角的和、差关系,有:
$\angle BOC = \angle AOB - \angle AOC$。
将已知的角度值代入上式,得:
$\angle BOC = 78^\circ - 42^\circ = 36^\circ$。
答案:C.$36^\circ$。
2. 在平面内,∠AOB= 60°,∠COB= 30°,则∠AOC= (
A.30°;
B.30°或60°;
C.30°或90°;
D.90°.
C
)A.30°;
B.30°或60°;
C.30°或90°;
D.90°.
答案:
解析:我们需要分析∠AOB和∠COB的位置关系来确定∠AOC的可能度数。
1. 当$OC$在$\angle AOB$内部时:
$\angle AOC = \angle AOB - \angle COB= 60^\circ - 30^\circ= 30^\circ$
2. 当$OC$在$\angle AOB$外部时:
$\angle AOC = \angle AOB + \angle COB= 60^\circ + 30^\circ= 90^\circ$
综合以上两种情况,$\angle AOC$的可能度数为$30^\circ$或$90^\circ$。
答案:C. $30^\circ$或$90^\circ$。
1. 当$OC$在$\angle AOB$内部时:
$\angle AOC = \angle AOB - \angle COB= 60^\circ - 30^\circ= 30^\circ$
2. 当$OC$在$\angle AOB$外部时:
$\angle AOC = \angle AOB + \angle COB= 60^\circ + 30^\circ= 90^\circ$
综合以上两种情况,$\angle AOC$的可能度数为$30^\circ$或$90^\circ$。
答案:C. $30^\circ$或$90^\circ$。
3. 下列各角不能用一副三角尺画出的是 (
A.105°;
B.145°;
C.75°;
D.15°.
B
)A.105°;
B.145°;
C.75°;
D.15°.
答案:
解析:本题考查的知识点是角的和、差计算以及三角尺上角度的认识。需要用三角尺上现有的角度通过相加或相减来画出给定的角度。
A选项:因为$45^{\circ}+60^{\circ}=105^{\circ}$,所以$105^{\circ}$角能用一副三角尺画出;
B选项:一副三角尺上的角度有$30^{\circ}$、$45^{\circ}$、$60^{\circ}$和$90^{\circ}$,无论如何组合相加或相减,都不能得到$145^{\circ}$,所以$145^{\circ}$角不能用一副三角尺画出;
C选项:因为$30^{\circ}+45^{\circ}=75^{\circ}$,所以$75^{\circ}$角能用一副三角尺画出;
D选项:因为$45^{\circ}-30^{\circ}=15^{\circ}$,所以$15^{\circ}$角能用一副三角尺画出。
答案:B。
A选项:因为$45^{\circ}+60^{\circ}=105^{\circ}$,所以$105^{\circ}$角能用一副三角尺画出;
B选项:一副三角尺上的角度有$30^{\circ}$、$45^{\circ}$、$60^{\circ}$和$90^{\circ}$,无论如何组合相加或相减,都不能得到$145^{\circ}$,所以$145^{\circ}$角不能用一副三角尺画出;
C选项:因为$30^{\circ}+45^{\circ}=75^{\circ}$,所以$75^{\circ}$角能用一副三角尺画出;
D选项:因为$45^{\circ}-30^{\circ}=15^{\circ}$,所以$15^{\circ}$角能用一副三角尺画出。
答案:B。
4. 两个锐角的和 (
A.一定是锐角;
B.一定是直角;
C.一定是钝角;
D.可能是钝角、直角或锐角.
D
)A.一定是锐角;
B.一定是直角;
C.一定是钝角;
D.可能是钝角、直角或锐角.
答案:
解:锐角是大于0°且小于90°的角。
情况1:两个较小锐角相加,如30°+40°=70°,和为锐角;
情况2:两个锐角相加等于90°,如30°+60°=90°,和为直角;
情况3:两个较大锐角相加,如60°+70°=130°,和为钝角。
结论:两个锐角的和可能是钝角、直角或锐角。
答案:D
情况1:两个较小锐角相加,如30°+40°=70°,和为锐角;
情况2:两个锐角相加等于90°,如30°+60°=90°,和为直角;
情况3:两个较大锐角相加,如60°+70°=130°,和为钝角。
结论:两个锐角的和可能是钝角、直角或锐角。
答案:D
5. 如图,∠AOC和∠BOD都是直角.若∠AOB= 140°,则∠DOC的度数是 (
A.30°;
B.40°;
C.50°;
D.60°.
B
)A.30°;
B.40°;
C.50°;
D.60°.
答案:
解:
∵∠AOC是直角,
∴∠AOC=90°,
∵∠AOB=140°,
∴∠BOC=∠AOB - ∠AOC=140° - 90°=50°,
∵∠BOD是直角,
∴∠BOD=90°,
∴∠DOC=∠BOD - ∠BOC=90° - 50°=40°,
答案:B.
∵∠AOC是直角,
∴∠AOC=90°,
∵∠AOB=140°,
∴∠BOC=∠AOB - ∠AOC=140° - 90°=50°,
∵∠BOD是直角,
∴∠BOD=90°,
∴∠DOC=∠BOD - ∠BOC=90° - 50°=40°,
答案:B.
6. 如图,∠EAD= ∠EAB-
∠BAD
,∠CAB+∠EAC=∠EAB
,∠DAC=180°
-∠EAD
-∠EAC
.
答案:
1. 首先看$\angle EAD=\angle EAB - \underline{\quad}$:
观察图形可知,$\angle EAD=\angle EAB-\angle BAD$。
2. 然后看$\angle CAB+\angle EAC=\underline{\quad}$:
根据角的加法,$\angle CAB+\angle EAC=\angle EAB$。
3. 最后看$\angle DAC=\underline{\quad}-\underline{\quad}-\underline{\quad}$:
观察图形可得$\angle DAC = 180^{\circ}-\angle EAD-\angle EAC$(答案不唯一,也可根据其他角的组合表示)。
故答案依次为:$\angle BAD$;$\angle EAB$;$180^{\circ}$;$\angle EAD$;$\angle EAC$(答案不唯一)。
观察图形可知,$\angle EAD=\angle EAB-\angle BAD$。
2. 然后看$\angle CAB+\angle EAC=\underline{\quad}$:
根据角的加法,$\angle CAB+\angle EAC=\angle EAB$。
3. 最后看$\angle DAC=\underline{\quad}-\underline{\quad}-\underline{\quad}$:
观察图形可得$\angle DAC = 180^{\circ}-\angle EAD-\angle EAC$(答案不唯一,也可根据其他角的组合表示)。
故答案依次为:$\angle BAD$;$\angle EAB$;$180^{\circ}$;$\angle EAD$;$\angle EAC$(答案不唯一)。
7. 若一副三角尺按如图所示的方式放置,则∠α+∠β= ______.

90°
答案:
解:一副三角尺的内角分别为 90°、60°、30°和 90°、45°、45°。图中两个三角尺的直角顶点重合,∠α与∠β所在的两个直角三角形的另外两个锐角之和为 90°,所以∠α + ∠β = 90°。
90°
90°
8. 已知∠α= 90°,∠β= 35°20',则∠α-∠β=
54°40'
,3∠β= 106°
.
答案:
解析:
本题主要考查角度的加减以及数乘运算。
对于$\angle\alpha - \angle\beta$:
首先,将$\angle\alpha$和$\angle\beta$都转换为度的小数形式以便进行减法运算。
$\angle\alpha = 90^\circ = 90^\circ 0'$
$\angle\beta = 35^\circ 20' = 35 + \frac{20}{60} = 35 + \frac{1}{3} \approx 35.3333^\circ$ (为精确起见,我们保留更多小数位,但在最后答案中会按题目要求格式给出)
然后进行减法运算:
$\angle\alpha - \angle\beta = 90^\circ - 35^\circ 20' = 54^\circ 40'$
对于$3\angle\beta$:
直接进行数乘运算:
$3\angle\beta = 3 × 35^\circ 20' = 105^\circ 60' = 106^\circ 0' = 106^\circ$
答案:
$54^\circ 40'$;$106^\circ$。
本题主要考查角度的加减以及数乘运算。
对于$\angle\alpha - \angle\beta$:
首先,将$\angle\alpha$和$\angle\beta$都转换为度的小数形式以便进行减法运算。
$\angle\alpha = 90^\circ = 90^\circ 0'$
$\angle\beta = 35^\circ 20' = 35 + \frac{20}{60} = 35 + \frac{1}{3} \approx 35.3333^\circ$ (为精确起见,我们保留更多小数位,但在最后答案中会按题目要求格式给出)
然后进行减法运算:
$\angle\alpha - \angle\beta = 90^\circ - 35^\circ 20' = 54^\circ 40'$
对于$3\angle\beta$:
直接进行数乘运算:
$3\angle\beta = 3 × 35^\circ 20' = 105^\circ 60' = 106^\circ 0' = 106^\circ$
答案:
$54^\circ 40'$;$106^\circ$。
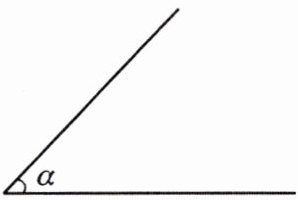
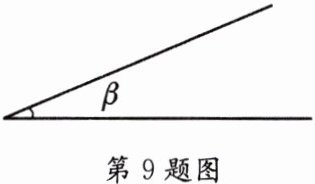
9. 如图,已知∠α,∠β,用量角器画一个角,使它等于∠α+2∠β.


答案:

查看更多完整答案,请扫码查看


