《2025年中学生世界六年级数学上册沪教版五四制》

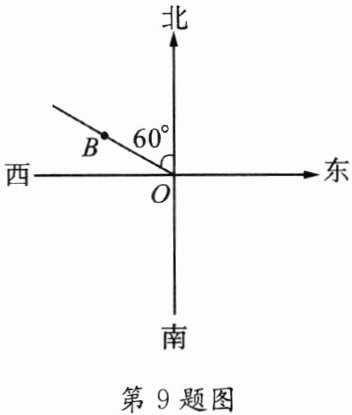
9. 如图,图中点 O 表示人民广场,点 B 表示真如镇,如果徐家汇在人民广场的西南方向,在真如镇的正南方向,试确定徐家汇的位置(用点 C 表示).

答案：

10. 如图,在小明画的一张地图上有 A,B,C 三地,因被墨迹污染,C 地具体位置看不清楚了.但是知道 C 地在 A 地的北偏东 30°,在 B 地的南偏东 45°,请你确定 C 地的位置.

答案：

11. 根据下列图形,回答角的个数.

(1)角的个数：图②：1+2=3,图③：1+2+3=6,图④：1+2+3+4=10；
(2)对照图形和算式,你能利用规律算出第 8 个图中一共有多少个角吗？
第 8 个图中一共有 36 个角。

答案： 解析：本题考查通过寻找图形规律来计算角的个数。
（1）图②：$1 + 2 = 3$；图③：$1 + 2 + 3 = 6$；图④：$1 + 2 + 3 + 4 = 10$。
故答案为：3；6；10。
（2）第$n$个图中角的个数为$1 + 2 + 3 + \cdots + n$。
根据等差数列求和公式$S_n=\frac{n(n + 1)}{2}$，当$n = 8$时，$S_8=\frac{8×(8 + 1)}{2}=\frac{8×9}{2}= 36$（个）。
答案：第 8 个图中一共有 36 个角。

思维与拓展 29
∠α,∠β,∠γ中有两个锐角和一个钝角,其数值已经给出,在计算$\frac{1}{15}(∠α+∠β+∠γ)$的值时,有三位同学分别算出了 23°,24°,25°这三个不同的结果.其中只有一个是正确的答案,这个正确答案是______.23°

答案： 解：设∠α+∠β+∠γ=x。
因为∠α,∠β,∠γ中有两个锐角和一个钝角，
所以 0°＜锐角＜90°，90°＜钝角＜180°，
则 0°+0°+90°＜x＜90°+90°+180°，即 90°＜x＜360°。
所以 $\frac{1}{15}×90°＜\frac{1}{15}x＜\frac{1}{15}×360°$，即 6°＜$\frac{1}{15}x$＜24°。
因为三位同学算出的结果分别为 23°，24°，25°，其中只有 23°在 6°到 24°之间，
所以正确答案是 23°。
23°