《2025年中学生世界六年级数学上册沪教版五四制》

11. 某车间有22名工人,每人每天可以生产1200个螺钉或2000个螺母,1个螺钉配2个螺母,为使每天生产的螺钉和螺母刚好配套,应该怎样安排生产螺钉和螺母的工人？

答案： 解：设安排$x$名工人生产螺钉，则安排$(22 - x)$名工人生产螺母。
根据题意，得$2×1200x = 2000(22 - x)$。
解得$x = 10$。
$22 - x = 22 - 10 = 12$。
答：应该安排10名工人生产螺钉，12名工人生产螺母。

12. 有一所寄宿制学校,计划安排学生宿舍时,如果每间安排住4人,那么将正好空出5间宿舍；如果每间安排住3人,那么将有100人没有床位.问：这所学校共有多少名学生住宿？共有多少间学生宿舍？

答案： 解析：
本题考查的是一元一次方程的应用。
设学校共有 x 间学生宿舍。
根据如果每间安排住4人，那么将正好空出5间宿舍，可得学生人数为4(x - 5)。
根据如果每间安排住3人，那么将有100人没有床位，可得学生人数为3x + 100。
根据学生人数相等，可得：
4(x - 5) = 3x + 100
解方程，化简得：4x-20=3x+100，
方程两边同时减去3x，加上20得：x=120。
所以学生人数为：4 × (120 - 5) = 460-20+4×5=440+20= 460-20+20=460（名）。
所以，这所学校共有 460 名学生住宿，共有 120 间学生宿舍。
答案：
解：设学校共有 x 间学生宿舍。
4(x - 5) = 3x + 100
4x-20=3x+100
4x-3x=100+20
x=120
4 × (120 - 5) = 460（名）
答：这所学校共有 460 名学生住宿，共有 120 间学生宿舍。

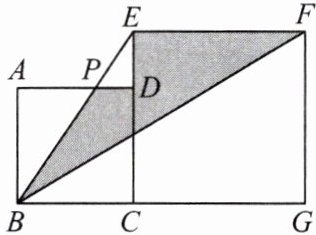
这道题是：大、小两个正方形并排放在一起,如图,这两个正方形的边长分别是12 cm和16 cm,求图中阴影部分的面积.

答案： 解析：本题可通过分析阴影部分与其他图形的关系，利用三角形面积公式来求解阴影部分的面积。
阴影部分是一个三角形，其底为小正方形的边长，高为大正方形与小正方形边长之和减去小正方形边长，即大正方形的边长。
先分别明确小正方形和大正方形的边长，再根据三角形面积公式$S = \frac{1}{2}ah$（其中$a$为底，$h$为高）来计算阴影部分面积。
答案：小正方形边长$a = 12$cm，大正方形边长$b = 16$cm。
阴影部分三角形的底为小正方形边长$12$cm，高为大正方形边长$16$cm。
根据三角形面积公式$S=\frac{1}{2}ah$，这里$a = 12$cm，$h = 16$cm，则$S=\frac{1}{2}×12×16 = 96$（$cm^{2}$）。
所以阴影部分的面积是$96cm^{2}$。