《2025年一遍过五年级数学上册苏教版》

1 填表。

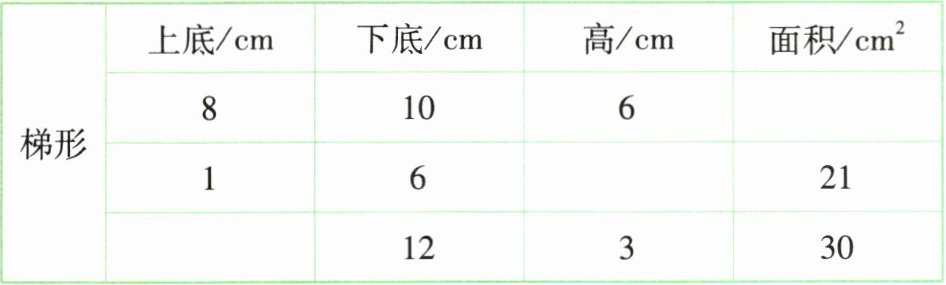
答案： （从上往下）54 6 8

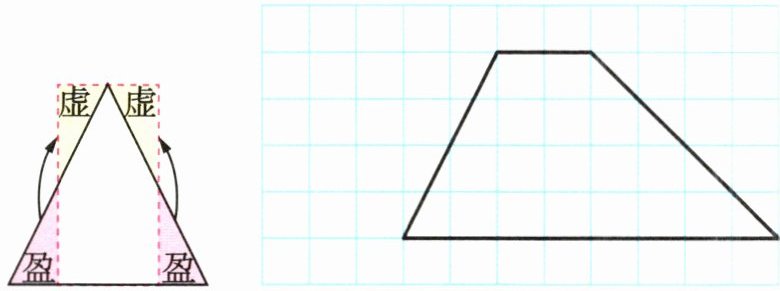
2 (情境题·文化情境)我国古代著名数学家刘徽在《九章算术》的注文中用“以盈补虚”的方法将三角形转化成长方形(如下面左图),请你将下面右图方格纸中的梯形也用“以盈补虚”的方法转化成长方形。
(1)转化后的长方形的长等于梯形的( ),
宽等于梯形的( ),长方形的面积与梯形的面积( )。(最后一空填“相等”或“不相等”)
(2)若每个小方格都是边长表示1厘米的正方形,
则这个梯形的面积是( )平方厘米。

答案：
转化成的长方形如图所示:

(1)上、下底之和的一半 高 相等 （2）20

3 下图中的梯形是由一张长方形纸片折叠而成的。这个梯形的面积是多少平方厘米?

答案： 7+3+3=13（厘米）
（7+13）×4÷2=40（平方厘米）
答：这个梯形的面积是40平方厘米。

4 一张梯形铁皮的上底是6分米,下底是12分米,高是8分米。如果在这张梯形铁皮中裁去一个最大的平行四边形,那么剩下的铁皮的面积是多少平方分米?如果裁去的是一个最大的三角形呢?
先根据题意分别画图,再解答!

答案：
画法不唯一，如:
（单位：分米）
（12-6）×8÷2=24（平方分米）
6×8÷2=24（平方分米）
答：裁去一个最大的平行四边形，剩下的铁皮的面积是24平方分米；裁去一个最大的时候三角形，剩下的铁皮的面积是的24平方分米。

5 两个相同的直角三角形有一部分重叠在一起(如图)。若AB长16厘米,AG长6厘米,BE长8厘米,则阴影部分的面积是多少平方厘米?
视频讲解

答案： （16-6+16）×8÷2=104（平方厘米）
答：阴影部分的面积是104平方厘米。
解析 因为三角形ABC和三角形DEF相同，所以它们同时减去三角形GBF，剩下部分的面积相等，故阴影部分的面积=梯形GBED的面积。