《2025年启东中学作业本九年级物理上册江苏版》

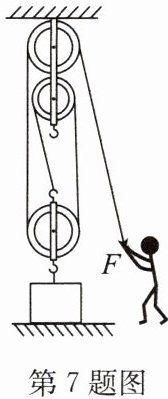
7. 如图所示,工人用滑轮组提升重物,已知重物的重力 $ G_{物} = 1000N $,动滑轮的重力 $ G_{动} = 200N $.在工人用力 F 作用下,重物匀速上升,30s 达到规定高度 6m 处.不计绳重和机械之间的摩擦.求:
(1)拉力做功的功率.
(2)滑轮组的机械效率.
(3)若用该装置提升另一重物时,机械效率达到 90%,则该重物的重力是多少?

答案： 解:
(1)有用功 $ W_{有用} = G_{物}h = 1000N×6m = 6000J $，
额外功 $ W_{额外} = G_{动}h = 200N×6m = 1200J $，
总功 $ W_{总} = W_{有用} + W_{额外} = 6000J + 1200J = 7200J $，
拉力做功的功率 $ P = \frac{W_{总}}{t} = \frac{7200J}{30s} = 240W $。
(2)滑轮组的机械效率
$ \eta = \frac{W_{有用}}{W_{总}}×100\% = \frac{6000J}{7200J}×100\% ≈ 83.3\% $。
(3)由 $ \eta = \frac{W_{有用}}{W_{总}}×100\% = \frac{G_{物}h}{G_{物}h + G_{动}h}×100\% = \frac{G_{物}}{G_{物} + G_{动}}×100\% $ 可知，
$ 90\% = \frac{G'_{物}}{G'_{物} + 200N} $，解得 $ G'_{物} = 1800N $，
即该重物的重力是 1800N。

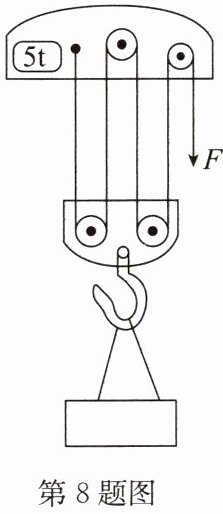
8. (2024·苏州)某起重机的滑轮组结构示意如图所示,其最大载重为 5t.起重机将 3600kg 的钢板匀速提升到 10m 高的桥墩上,滑轮组的机械效率为 80%.不计钢丝绳的重力和摩擦,g 取 10N/kg.求:
(1)克服钢板重力做的功 $ W_{有用} $.
(2)钢丝绳的拉力 F.
(3)滑轮组满载时的机械效率(保留一位小数).

答案： 解:
(1)钢板的重力
$ G_{钢板} = m_{钢板}g = 3600kg×10N/kg = 3.6×10^{4}N $。
克服钢板重力做的功
$ W_{有用} = G_{钢板}h = 3.6×10^{4}N×10m = 3.6×10^{5}J $。
(2)滑轮组共有 4 段绳子拉着动滑轮，故拉力移动的距离为钢板提升高度的 4 倍，即 $ s = 40m $，
拉力做的功 $ W_{总} = \frac{W_{有用}}{\eta} = \frac{3.6×10^{5}J}{80\%} = 4.5×10^{5}J $，
钢丝绳的拉力 $ F = \frac{W_{总}}{s} = \frac{4.5×10^{5}J}{40m} = 1.125×10^{4}N $。
(3)$ W_{额外} = W_{总} - W_{有用} = 4.5×10^{5}J - 3.6×10^{5}J = 9×10^{4}J $，
动滑轮的重力 $ G_{动} = \frac{W_{额外}}{h} = \frac{9×10^{4}J}{10m} = 9×10^{3}N $。
当载重最大时，质量为 $ 5t = 5×10^{3}kg $， $ G_{最大} = mg = 5×10^{3}kg×10N/kg = 5×10^{4}N $，
滑轮组满载时的机械效率
$ \eta' = \frac{W'_{有用}}{W'_{总}}×100\% = \frac{G_{最大}h'}{(G_{最大} + G_{动})h'}×100\% = \frac{G_{最大}}{G_{最大} + G_{动}} = \frac{5×10^{4}N}{5×10^{4}N + 9×10^{3}N}×100\% ≈ 84.7\% $。

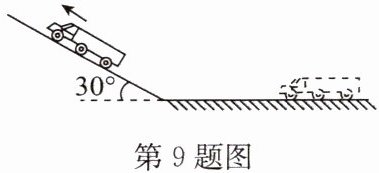
9. 如图所示,重为 $ 3.2 × 10^4N $ 的卡车,经过一段水平路面,再以 $ 9.6 × 10^4W $ 的功率匀速爬上高 5m、长 10m 的斜坡,已知斜坡的机械效率为 80%.求:
(1)卡车爬坡时牵引力所做的总功.
(2)卡车爬坡时的速度.

答案： 解:
(1)卡车爬坡时，有用功
$ W_{有用} = Gh = 3.2×10^{4}N×5m = 1.6×10^{5}J $，
由 $ \eta = \frac{W_{有用}}{W_{总}}×100\% $ 可得，卡车爬坡时牵引力所做的总功
$ W_{总} = \frac{W_{有用}}{\eta} = \frac{1.6×10^{5}J}{80\%} = 2×10^{5}J $。
(2)由 $ W = Fs $ 可得，汽车的牵引力
$ F = \frac{W_{总}}{s} = \frac{2×10^{5}J}{10m} = 2×10^{4}N $，
根据 $ P = \frac{W}{t} = \frac{Fs}{t} = Fv $ 可得，卡车爬坡时的速度
$ v = \frac{P}{F} = \frac{9.6×10^{4}W}{2×10^{4}N} = 4.8m/s $。