《2025年华东师大版一课一练七年级数学上册沪教版五四制》

1 下列现象:①地下水位逐年下降;②传送带的移动;③方向盘的转动;④水龙头开关的转动;⑤钟摆的运动;⑥荡秋千运动,是旋转的有( )。

A.2个
B.3个
C.4个
D.5个

答案： 解：③方向盘的转动、④水龙头开关的转动、⑤钟摆的运动、⑥荡秋千运动是旋转，共4个。
答案：C

2 在俄罗斯方块游戏中,出现的图案可进行顺时针、逆时针旋转或向左、向右平移,如图是已拼好的图案,现又出现一个形如“L”的方块正向下运动,你必须进行( )操作,才能拼成一个长方形。

A.顺时针旋转90°,向右平移
B.逆时针旋转90°,向右平移
C.顺时针旋转90°,向左平移
D.逆时针旋转90°,向左平移

答案： 【解析】：
本题考查图形的旋转与平移。
观察图形，要将形如“L”的方块拼成一个长方形，需要先将“L”形方块进行旋转，使其方向与已拼好的图案中的空缺部分相匹配，然后再进行平移，使其与已拼好的图案完全重合。
形如“L”的方块，如果顺时针旋转$90^\circ$，它的方向会与已拼好的图案中的空缺部分相匹配，接下来需要将旋转后的“L”形方块向右平移，使其与已拼好的图案完全重合，形成长方形。
如果逆时针旋转$90^\circ$，则方向不匹配，向左平移也无法使“L”形方块与已拼好的图案完全重合。
所以，必须进行顺时针旋转$90^\circ$，再向右平移的操作，才能拼成一个长方形。
【答案】：A

3 如图①是中国数学会的会徽,它是由四个相同的直角三角形拼成的正方形。将会徽抽象为图②,已知BF= a,AF= b,AB= c,将图②进行图形运动得到图③,那么下面的说法不正确的是( )。




A.△BMC可由△BFA绕点B顺时针旋转90°得到
B.△BMC可由△AED沿HC方向平移距离a,再沿CM方向平移距离b得到
C.△DCN可以看作由△DAE绕点D逆时针旋转90°得到
D.如果正方形ABCD与六边形MNDEFB的面积相等,那么c^{2}= 2ab+(b-a)^{2}

答案： 【解析】：
本题主要考查图形的旋转、平移以及面积计算等知识点。
选项A：
观察图②和图③，可以发现$\triangle BMC$与$\triangle BFA$有相同的边和角，且$\triangle BMC$可由$\triangle BFA$绕点$B$顺时针旋转$90^\circ$得到，所以选项A是正确的。
选项B：
对于$\triangle BMC$，如果由$\triangle AED$进行平移得到，应该先沿$GD$方向平移距离$a$，再沿$CG$方向平移距离$b$，而不是沿$HC$方向平移距离$a$，再沿$CM$方向平移距离$b$。因此，选项B是不正确的。
选项C：
观察图②和图③，可以发现$\triangle DCN$与$\triangle DAE$有相同的边和角，且$\triangle DCN$可以看作由$\triangle DAE$绕点$D$逆时针旋转$90^\circ$得到，所以选项C是正确的。
选项D：
如果正方形$ABCD$与六边形$MNDEFB$的面积相等，那么可以通过计算面积来验证这个等式。
正方形$ABCD$的面积为$c^2$。
六边形$MNDEFB$的面积可以看作是由正方形$ABCD$的面积减去四个直角三角形的面积再加上一个小正方形$(b-a)^2$的面积。
即：$c^2 = 4×\frac{1}{2}ab + (b-a)^2 = 2ab + (b-a)^2$。
所以选项D是正确的。
【答案】：B。

4 如图,在Rt△ABC中,∠C= 90°,∠ABC= 60°,将Rt△ABC绕点B顺时针旋转一个角度到△A'B'C'的位置,使得点A、B、C'在同一直线上,那么这个旋转的角度是____。

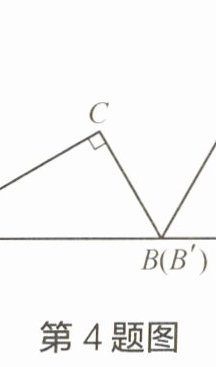
答案： 解：在Rt△ABC中，∠C=90°，∠ABC=60°，
∴∠BAC=30°。
∵△A'B'C'是由Rt△ABC绕点B顺时针旋转得到，
∴∠A'BC'=∠ABC=60°，BC=BC'。
∵点A、B、C'在同一直线上，
∴∠ABC'=180°。
∴旋转角∠CBC'=∠ABC'-∠ABC=180°-60°=120°。
120°

5 在如图所示的四个图案中,旋转90°后能与本身重合的图案有____个。

答案： 答案略