第67页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
10. 两个相同的烧杯中分别装满了两种不同的液体,把甲、乙两球分别轻轻放入两杯液体,最后处于如图所示状态。甲、乙排开液体的重力相等,甲、乙所受浮力相比(
A.甲所受浮力更大
B.乙所受浮力更大
C.甲、乙所受浮力一样大
D.不知道液体密度无法比较浮力大小
C
)A.甲所受浮力更大
B.乙所受浮力更大
C.甲、乙所受浮力一样大
D.不知道液体密度无法比较浮力大小
答案:
C 解析:根据阿基米德原理可知,物体所受浮力的大小等于排开液体的重力,因为甲、乙排开液体的重力相等,故甲、乙受到的浮力相等。故选C。
11. 水平面上有两个相同的溢水杯,分别装满不同的液体,将同一个小球分别放入溢水杯中静止时(如图所示),从甲杯中溢出了0.6N的液体,从乙杯中溢出了0.4N的液体。下列说法不正确的是(
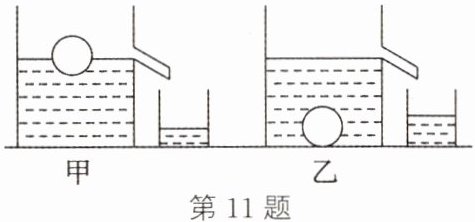
A.小球在甲杯中受到的浮力大于在乙杯中受到的浮力
B.小球的重力等于0.6N,在乙杯中受到的浮力等于0.4N
C.甲杯液体的密度大于乙杯液体的密度
D.小球放入前,液体对甲杯底的压强等于液体对乙杯底的压强
D
)
A.小球在甲杯中受到的浮力大于在乙杯中受到的浮力
B.小球的重力等于0.6N,在乙杯中受到的浮力等于0.4N
C.甲杯液体的密度大于乙杯液体的密度
D.小球放入前,液体对甲杯底的压强等于液体对乙杯底的压强
答案:
D
12. 一弹簧测力计下挂一圆柱体,将圆柱体从盛有水的烧杯上方离水面某一高度处缓慢下降,然后将圆柱体逐渐浸入水中。如图是整个过程中弹簧测力计的示数F与圆柱体下降高度h变化关系的图像。下列说法正确的是(g取$10\ N/kg$)(
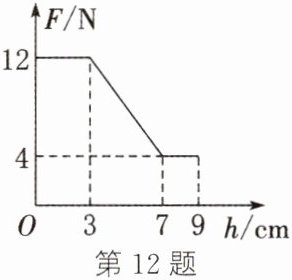
A.圆柱体的密度是$2.0× 10^{3}\ kg/m^{3}$
B.圆柱体的体积为$8× 10^{-4}\ m^{3}$
C.圆柱体受到的重力是8N
D.圆柱体受到的最大浮力是4N
B
)
A.圆柱体的密度是$2.0× 10^{3}\ kg/m^{3}$
B.圆柱体的体积为$8× 10^{-4}\ m^{3}$
C.圆柱体受到的重力是8N
D.圆柱体受到的最大浮力是4N
答案:
B
13. 将一石块挂在弹簧测力计下,并分别浸没在水和盐水中,弹簧测力计静止时示数如图所示,g取$10\ N/kg$。
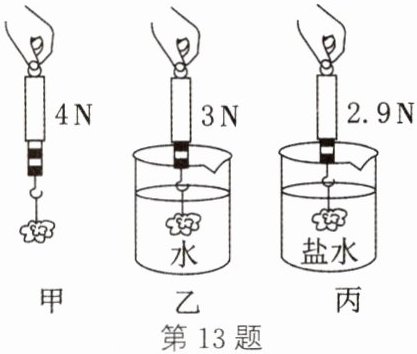
(1)求石块在水中所受浮力。
(2)求小石块的密度。
(3)求盐水的密度。

(1)求石块在水中所受浮力。
(2)求小石块的密度。
(3)求盐水的密度。
答案:
1. (1)求石块在水中所受浮力:
解:根据称重法测浮力$F_{浮}=G - F_{示}$,由图甲知$G = 4N$,图乙知$F_{示水}=3N$。
则石块在水中所受浮力$F_{浮水}=G - F_{示水}=4N - 3N = 1N$。
2. (2)求小石块的密度:
解:由$F_{浮}=\rho_{液}gV_{排}$,石块浸没在水中,$V = V_{排}$,$F_{浮水}=\rho_{水}gV$,可得$V=\frac{F_{浮水}}{\rho_{水}g}$。
已知$\rho_{水}=1×10^{3}kg/m^{3}$,$g = 10N/kg$,$F_{浮水}=1N$,则$V=\frac{1N}{1×10^{3}kg/m^{3}×10N/kg}=1×10^{-4}m^{3}$。
又因为$G = mg$,$m=\frac{G}{g}$,$G = 4N$,$g = 10N/kg$,所以$m=\frac{4N}{10N/kg}=0.4kg$。
根据$\rho=\frac{m}{V}$,可得$\rho=\frac{0.4kg}{1×10^{-4}m^{3}} = 4×10^{3}kg/m^{3}$。
3. (3)求盐水的密度:
解:石块浸没在盐水中,$F_{浮盐}=G - F_{示盐}$,由图丙知$F_{示盐}=2.9N$,$G = 4N$,则$F_{浮盐}=4N - 2.9N = 1.1N$。
因为$F_{浮}=\rho_{液}gV_{排}$,$V_{排}=V = 1×10^{-4}m^{3}$,$F_{浮盐}=\rho_{盐水}gV$,所以$\rho_{盐水}=\frac{F_{浮盐}}{gV}$。
把$F_{浮盐}=1.1N$,$g = 10N/kg$,$V = 1×10^{-4}m^{3}$代入可得$\rho_{盐水}=\frac{1.1N}{10N/kg×1×10^{-4}m^{3}}=1.1×10^{3}kg/m^{3}$。
综上,(1)石块在水中所受浮力为$1N$;(2)小石块的密度为$4×10^{3}kg/m^{3}$;(3)盐水的密度为$1.1×10^{3}kg/m^{3}$。
解:根据称重法测浮力$F_{浮}=G - F_{示}$,由图甲知$G = 4N$,图乙知$F_{示水}=3N$。
则石块在水中所受浮力$F_{浮水}=G - F_{示水}=4N - 3N = 1N$。
2. (2)求小石块的密度:
解:由$F_{浮}=\rho_{液}gV_{排}$,石块浸没在水中,$V = V_{排}$,$F_{浮水}=\rho_{水}gV$,可得$V=\frac{F_{浮水}}{\rho_{水}g}$。
已知$\rho_{水}=1×10^{3}kg/m^{3}$,$g = 10N/kg$,$F_{浮水}=1N$,则$V=\frac{1N}{1×10^{3}kg/m^{3}×10N/kg}=1×10^{-4}m^{3}$。
又因为$G = mg$,$m=\frac{G}{g}$,$G = 4N$,$g = 10N/kg$,所以$m=\frac{4N}{10N/kg}=0.4kg$。
根据$\rho=\frac{m}{V}$,可得$\rho=\frac{0.4kg}{1×10^{-4}m^{3}} = 4×10^{3}kg/m^{3}$。
3. (3)求盐水的密度:
解:石块浸没在盐水中,$F_{浮盐}=G - F_{示盐}$,由图丙知$F_{示盐}=2.9N$,$G = 4N$,则$F_{浮盐}=4N - 2.9N = 1.1N$。
因为$F_{浮}=\rho_{液}gV_{排}$,$V_{排}=V = 1×10^{-4}m^{3}$,$F_{浮盐}=\rho_{盐水}gV$,所以$\rho_{盐水}=\frac{F_{浮盐}}{gV}$。
把$F_{浮盐}=1.1N$,$g = 10N/kg$,$V = 1×10^{-4}m^{3}$代入可得$\rho_{盐水}=\frac{1.1N}{10N/kg×1×10^{-4}m^{3}}=1.1×10^{3}kg/m^{3}$。
综上,(1)石块在水中所受浮力为$1N$;(2)小石块的密度为$4×10^{3}kg/m^{3}$;(3)盐水的密度为$1.1×10^{3}kg/m^{3}$。
查看更多完整答案,请扫码查看


