《2025年实验班提优训练六年级数学上册北师大版》

5. 如右下图,正方形的边长是 2 厘米,圆的面积与正方形的面积的比是多少？

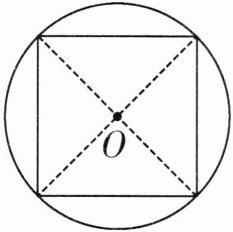
答案： 5.正方形的面积:$2×2=4$(平方厘米) 圆的面积:$3.14×(4÷2)=6.28$(平方厘米) 面积比:$6.28:4=628:400=157:100$

6. 有两个同心圆组成的圆环(如右下图),环宽恰好等于小圆的半径,求大圆的面积和涂色部分面积的比。

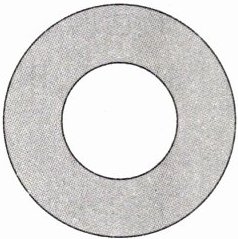
答案： 6.设小圆半径为1,则大圆半径为2,大圆面积为$3.14×2^{2}=12.56$,小圆面积为$3.14×1^{2}=3.14$,涂色部分面积为12.56-3.14=9.42,大圆面积和涂色部分面积的比为$12.56:9.42=4:3$。

7. 平行四边形 $ABCD$ 被分成甲、乙、丙三个三角形,已知 $BE= 28cm$,$EC= 16cm$,请你分别写出甲与乙、甲与丙、乙与丙的面积比。

答案： 7.$S_{甲}:S_{乙}=28:(28+16)=7:11$ $S_{甲}:S_{丙}=28:16=7:4$ $S_{乙}:S_{丙}=(28+16):16=11:4$ 【提示】根据甲、乙、丙三个三角形的高都相等可知:甲与乙、甲与丙、乙与丙的面积比等于三角形的高对应的各自底边长的比。

8. 如右下图,在 $\triangle ABC$ 中,已知 $AE= \frac{1}{3}AC$,$BD= \frac{1}{5}BC$,则涂色部分与空白部分面积的比是多少？

答案： 8.$BD:DC=1:(5-1)=1:4$ 三角形ABD的面积∶三角形ADC的面积=1∶4 假设三角形ABD的面积为1,则三角形ADC的面积为4。 $AE:EC=1:(3-1)=1:2$ 三角形ADE的面积∶三角形DEC的面积=1∶2 三角形ADE的面积:$4×\frac{1}{1+2}=\frac{4}{3}$ 三角形DEC的面积:$4×\frac{2}{1+2}=\frac{8}{3}$ 涂色部分面积∶空白部分面积=$\frac{4}{3}:(1+\frac{8}{3})=4:11$ 【提示】根据$BD:DC=1:4$可知,三角形ABD和三角形ADC的面积比,根据$AE:EC=1:2$可知,三角形ADE和三角形DEC的面积比,由此可求出涂色部分和空白部分的面积比。

9. 有四个杯子,里面放着不同质量的水(如下图),现在往每个杯子里面加入盐,要使每个杯子中的盐和盐水的最简整数比相同。如果在(1)号杯中加入 10 克的盐,那么应分别在其余几个杯子中加入多少克的盐？

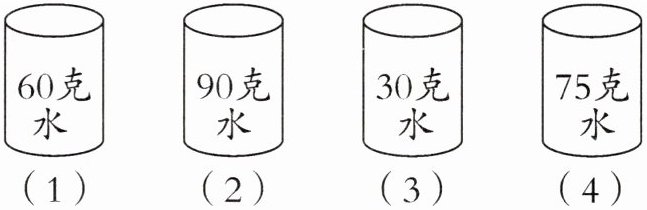
答案： 9.
(2)号杯加15克盐,
(3)号杯加5克盐,
(4)号杯加12.5克盐．【提示】在
(1)号杯子中加10克盐,这样
(1)号杯子中盐与盐水的质量比就是$10:(10 + 60)=10:70=1:7$。由题意可知,每个杯子里盐与盐水的比都是$1:7$,根据这个比,即可求出往其他几个杯子里加盐的克数。