《2025年实验班提优训练六年级数学上册北师大版》

1. 涂色表示下面的百分数。

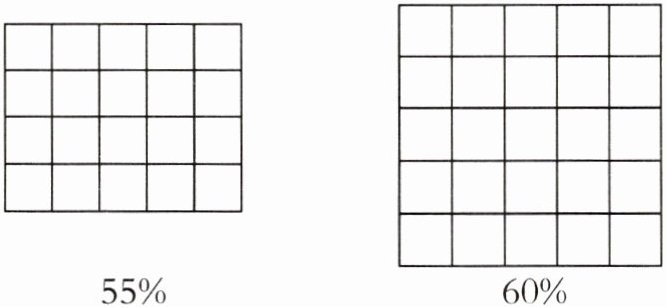
答案： 本题可根据百分数的意义，通过计算每个方格图中需要涂色的方格数量来进行涂色。
1. 分析第一个方格图（表示$55\%$）
观察第一个方格图可知，该方格图被平均分成了$20$个小方格。
根据百分数的意义，求一个数的百分之几是多少用乘法计算，那么需要涂色的方格数量为：$20×55\% = 20×0.55 = 11$（个）。
所以，在第一个方格图中涂$11$个小方格即可表示$55\%$。
2. 分析第二个方格图（表示$60\%$）
观察第二个方格图可知，该方格图同样被平均分成了$20$个小方格。
同理，需要涂色的方格数量为：$20×60\% = 20×0.6 = 12$（个）。
所以，在第二个方格图中涂$12$个小方格即可表示$60\%$。
综上，第一个方格图涂$11$个小方格，第二个方格图涂$12$个小方格（图略）。

2. 判一判。
(1)到银行取款时,银行多支付的钱叫作利息。 (对)
(2)实际消费 270 元,比计划节省 90 元,实际消费比计划节约了 25%。 (对)
(3)某产品的合格率达到 102%。 (错)

答案： 解析：
(1) 题目考查的是利息的定义。根据金融知识，利息是指借款人或存款人因使用资金而支付或获得的报酬。在银行存款的情境中，银行多支付的钱确实是利息。
(2) 题目考查的是百分数的应用。首先，我们需要计算出计划消费的金额，然后计算实际消费占计划消费的比例，最后判断这个比例是否等于75%（因为节省25%意味着实际消费是计划的75%）。计划消费金额 = 实际消费金额 + 节省的金额 = 270元 + 90元 = 360元。实际消费占计划消费的比例 = 实际消费金额 / 计划消费金额 = 270元 / 360元 = 0.75 = 75%。因此，实际消费比计划节约了25%是正确的。
(3) 题目考查的是合格率的计算和理解。合格率是指合格产品的数量占全部产品数量的比例。这个比例最高只能是100%，因为合格产品的数量不可能超过全部产品的数量。
答案：
(1) 对
(2) 对
(3) 错

3. 解方程。
$1 + 25\%x = 6.25$ $75\%x - \frac{2}{3}x = \frac{5}{6}$

答案： $1 + 25\%x = 6.25$
解：$25\%x = 6.25 - 1$
$25\%x = 5.25$
$x = 5.25÷25\%$
$x = 21$
$75\%x - \frac{2}{3}x = \frac{5}{6}$
解：$\frac{3}{4}x - \frac{2}{3}x = \frac{5}{6}$
$\frac{9}{12}x - \frac{8}{12}x = \frac{5}{6}$
$\frac{1}{12}x = \frac{5}{6}$
$x = \frac{5}{6}×12$
$x = 10$

4. 小军体重 35 kg,比小强重 25%,小强重多少千克？正确的列式是(D)。
A.$35×(1 - 25\%)$
B.$35×(1 + 25\%)$
C.$35÷(1 - 25\%)$
D.$35÷(1 + 25\%)$

答案： 解析：本题考查的是百分数除法的应用。小军体重35 kg，比小强重25%，即小军的体重是小强的（1+25%）。要求小强的体重，应该用小军的体重除以（1+25%）。
答案：D

5. 已经画了 40%,把方格图补充完整。

答案： 解析：本题考查了百分数与图形结合的知识点，需要明确整体方格数量以及已画部分占比，通过计算得出剩余部分占比，进而补充完整方格图。
答案：方格图一共$5×4=20$（个）小方格，
已画了$40\%$，即$20×40\%=8$（个）小方格，
那么还需要画$20-8=12$（个）小方格。
将剩下的$12$个小方格补充完整即可（补充方式不唯一），图略。

6. 有两杯盐水,第一杯 200 克含盐率是 20%,第二杯 100 克含盐率是 15%,将这两杯盐水混合后,新盐水的含盐率是多少？(百分号前保留一位小数)

答案： 第一杯盐的质量：200×20% = 40（克）
第二杯盐的质量：100×15% = 15（克）
混合后盐的总质量：40 + 15 = 55（克）
混合后盐水的总质量：200 + 100 = 300（克）
新盐水的含盐率：55÷300×100% ≈ 18.3%
答：新盐水的含盐率约是18.3%。

7. 新情境 葡萄干 葡萄干是借助于太阳热或人工加热使葡萄果实脱水形成的食品。现有 500 kg 新鲜葡萄,含水率为 95%,晾制若干天后含水率降至 80%,质量减少了的多少千克？(晾制过程中只减少葡萄中的水分)

答案： 解析：本题考查含水率相关知识，解题关键在于明确不变量是除水分外其他物质的质量。先算出原来葡萄中除水分外物质的质量，再根据晾制后含水率算出晾制后葡萄的总质量，最后用原来葡萄的质量减去晾制后葡萄的质量，即可得到质量减少的值。
1. 计算原来葡萄中除水分外物质的质量：
已知新鲜葡萄质量为$500kg$，含水率为$95\%$，那么除水分外物质占比为$(1 - 95\%)$，其质量为$500×(1 - 95\%)=500×0.05 = 25$（千克）。
2. 计算晾制后葡萄的总质量：
晾制后含水率降至$80\%$，则除水分外物质占比为$(1 - 80\%)$，因为晾制过程中只减少葡萄中的水分，所以除水分外物质质量不变，仍为$25$千克。
根据“已知一个数的百分之几是多少，求这个数用除法”，可得晾制后葡萄的总质量为$25÷(1 - 80\%)=25÷0.2 = 125$（千克）。
3. 计算质量减少的值：
原来葡萄质量为$500$千克，晾制后葡萄质量为$125$千克，所以质量减少了$500 - 125 = 375$（千克）。
答案：质量减少了$375$千克。

8. 仓库有一批水果,运出了 40%,又运进 300 千克,这时仓库中水果的质量是原来的$\frac{2}{3}$,原来仓库中的水果质量是多少?

答案： 解析：本题考查的是百分数和分数的应用。
假设原来仓库中的水果质量是 $x$ 千克。
运出了 40%，即运出了 $0.4x$ 千克。
这时仓库里剩下的水果质量是 $x - 0.4x = 0.6x$ 千克。
又运进 300 千克后，仓库中的水果质量变为 $0.6x + 300$ 千克。
根据这时仓库中水果的质量是原来的 $\frac{2}{3}$，可以列出方程：
$0.6x + 300 = \frac{2}{3}x$，
解这个方程：
等式两边同时减去$0.6x$得：$300 = \frac{2}{3}x - 0.6x$，
合并同类项得：$300 = \frac{2}{3}x - \frac{3}{5}x$，
通分得：$300 = \frac{10}{15}x - \frac{9}{15}x$，
化简得：$300 = \frac{1}{15}x$，
系数化$1$得：$x = 4500$。
所以，原来仓库中的水果质量是 4500 千克。

9. 小明看一本故事书,已经看了 30%,剩下的比已看的多 48 页,这本故事书共有多少页？请先在下面的线段图上把信息和问题补充完整,再列式解答。

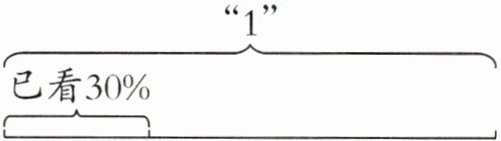
答案： 解析：本题考查百分数的实际应用，可通过分析已知条件，找出数量关系来求解故事书的总页数。
已知小明已经看了$30\%$，可以把这本书的总页数看作单位“$1$”，那么剩下的页数占比为$(1 - 30\%)$。
又已知剩下的比已看的多$48$页，所以剩下的页数占比减去已看的页数占比，对应的实际页数就是$48$页，由此可先算出$48$页占总页数的百分比，进而求出总页数。
答案：
线段图补充：在表示已看$30\%$的线段下方标注“已看$30\%$”，在剩下的线段部分标注“剩下$(1 - 30\%)$”，在剩下线段比已看线段多的部分标注“多$48$页”。
列式解答：
$1-30\% = 70\%$
$70\% - 30\% = 40\%$
$48÷40\% = 48÷0.4 = 120$（页）
答：这本故事书共有$120$页。