《2025年通成学典课时作业本一年级数学上册苏教版苏州专版》

1. 看图列式计算。
(1) $2 + 2 = 4$
(2) $5 + 0 = 5$ (或 $0 + 5 = 5$)
(3) $3 - 1 = 2$
(4) $5 - 2 = 3$
(5) $4 - 4 = 0$

答案： 1.
(1) $2 + 2 = 4$
(2) $5 + 0 = 5$ (或 $0 + 5 = 5$)
(3) $3 - 1 = 2$
(4) $5 - 2 = 3$
(5) $4 - 4 = 0$

2. 先画一画,再写出得数。

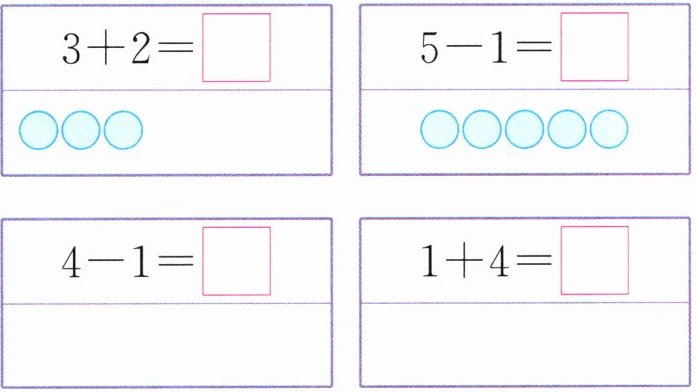
答案：
2.

3. 看图把算式补充完整。
(1)
$2+$2$=$4
(2)
$4-$2$=$2

答案： 3.
(1) 2 4
(2) 2 2

4. 连一连。

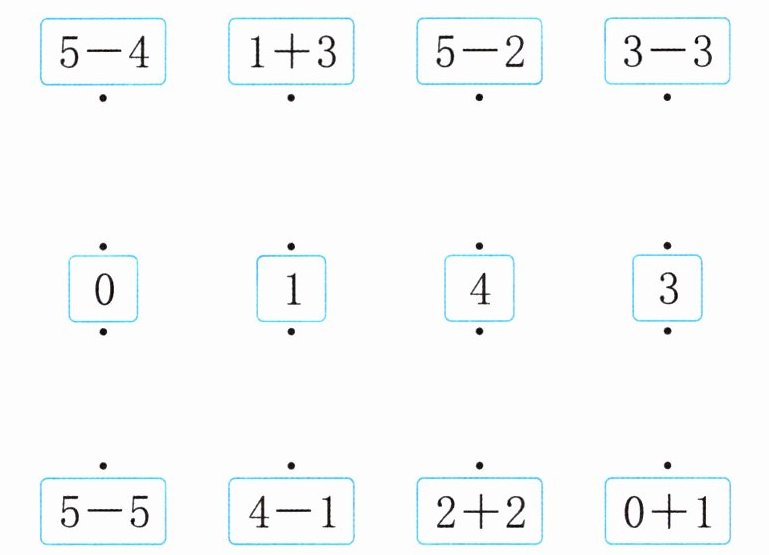
答案：
4.

5. 在$◯$里填“$＞$”“$＜$”或“$=$”。
$1+4$$=$$5-0$ $5-4$$＜$$2+2$
$3-2$$＜$$4-1$ $5-3$$=$$4-2$
$2+3$$＞$$5-1$ $3-0$$＞$$2+0$
$4-4$$＜$$5-2$ $5+0$$＞$$4-0$

答案： 5. $=$ $＜$ $＜$ $=$ $＞$ $＞$ $＜$ $＞$

$\begin{array}{l}\mathrm{桃}= (\color{red}{0})\\\mathrm{苹果}= (\color{red}{5})\end{array} $

答案： 6. 0 5

7.(思维过程)把0、1、2、3、4、5填在$□$里,使算式成立。(每组算式中,每个数只能用一次)
0+5=1+4=2+3
5-4=3-2=1-0(或5-2=4-1=3-0)

答案： 7. $0 + 5 = 1 + 4 = 2 + 3$ $5 - 4 = 3 - 2 = 1 - 0$ (或 $5 - 2 = 4 - 1 = 3 - 0$)
解析:第一组算式,把连续的数写成和相等的算式,因为每个数只能用一次,所以把最大的数和最小的数配成一对,第 2 大的数和第 2 小的数配成一对,以此类推,得 $0 + 5 = 1 + 4 = 2 + 3$。第二组算式,把连续的数写成差相等的算式,一般有两种方法,一种是相邻数相减都得 1;另一种是将连续的数按前一半和后一半分为两组,较大一组的数减较小一组的对应数的结果都是相等的。第一种方法可以得到 $5 - 4 = 3 - 2 = 1 - 0$,第二种方法可以得到 $5 - 2 = 4 - 1 = 3 - 0$。