《2025年5年中考3年模拟九年级数学上册北师大版》

9.「2025山东广饶期中,★☆」函数$ y = ( k ^ { 2 } + 2 k ) x ^ { k ^ { 2 } + k - 1 } $是反比例函数,则k的值为(B)
A.1
B.-1
C.0或-1
D.±1

答案： 9.B
∵函数y=(k²+2k)x^(k²+k-1)是反比例函数,
∴$\begin{cases} k²+2k≠0, \\ k²+k-1=-1, \end{cases}$解得k=-1.故选B.

10.「2024上海浦东新区期末,★☆」已知$ y = y _ { 1 } + y _ { 2 } $,并且$ y _ { 1 } 与 x - 1 $成正比例,$ y _ { 2 } $与x成反比例,当$ x = 2 $时,$ y = 5 $；当$ x = - 2 $时,$ y = - 9 $.
(1)求y关于x的函数解析式.
(2)求当$ x = 8 $时的y值.

答案： 10.解析
(1)因为y₁与x-1成正比例,所以设y₁=k₁(x-1)(k₁≠0).因为y₂与x成反比例,所以设y₂=$\frac{k₂}{x}$(k₂≠0).所以y=k₁(x-1)+$\frac{k₂}{x}$.因为当x=2时,y=5,当x=-2时,y=-9,所以$\begin{cases} 5=k₁+\frac{k₂}{2}, \\ -9=-3k₁-\frac{k₂}{2}, \end{cases}$解得$\begin{cases} k₁=2, \\ k₂=6. \end{cases}$所以y关于x的函数解析式为y=2(x-1)+$\frac{6}{x}$.
(2)当x=8时,y=2×7+$\frac{3}{4}$=$\frac{59}{4}$.

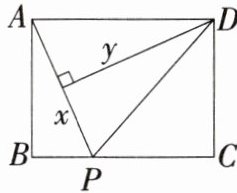
11.「★☆」如图,矩形ABCD中,$ A B = 3 $,$ B C = 4 $,动点P在BC上移动(不与点B,C重合).记$ P A = x $,点D到直线PA的距离为y,求y关于x的函数解析式,并写出自变量x的取值范围.

答案：
11.解析 如图,∠AED=90°,

∵四边形ABCD是矩形,
∴AD//BC,
∴∠DAE=∠APB,
∵∠B=∠AED=90°,
∴△ABP∽△DEA,
∴$\frac{DE}{AB}$=$\frac{AD}{AP}$,
∴$\frac{y}{3}$=$\frac{4}{x}$,
∴y=$\frac{12}{x}$.连接AC,
∵AB=3,BC=4,∠B=90°,
∴AC=$\sqrt{AB²+BC²}$=5,
∴自变量x的取值范围为3＜x＜5,故y=$\frac{12}{x}$(3＜x＜5).

12.新课标运算能力已知$ ( a - b + 3 ) ^ { 2 } + \sqrt { a + 2 b } = 0 $,则关于x的函数$ y = ( a - b ) x ^ { a + b } $是反比例函数,比例系数为-3.

答案： 12.答案 反比例;-3
解析
∵(a-b+3)²+$\sqrt{a+2b}$=0,(a-b+3)²≥0,$\sqrt{a+2b}$≥0,
∴$\begin{cases} a-b+3=0, \\ a+2b=0, \end{cases}$解得$\begin{cases} a=-2, \\ b=1. \end{cases}$
∴函数y=(a-b)x^(a+b)为y=-$\frac{3}{x}$,是反比例函数,比例系数为-3.

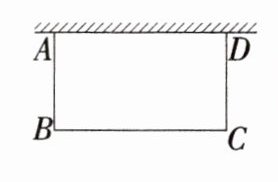
13.新课标应用意识如图,某校科技小组计划利用已有的一面长为6m的墙,用篱笆围一个面积为$ 30 \mathrm { m } ^ { 2 } $的矩形科技园ABCD,设AB的长为x m,BC的长为y m.
(1)求y关于x的函数表达式和自变量x的取值范围.
(2)边AD和DC的长都是整数,若围成矩形科技园ABCD的篱笆总长不超过20m,求出满足条件的所有围建方案.

答案： 13.解析
(1)依题意得xy=30,
∴y=$\frac{30}{x}$.又
∵墙长为6m,
∴$\frac{30}{x}$≤6,
∴x≥5.
∴y关于x的函数表达式为y=$\frac{30}{x}$(x≥5).
(2)
∵x,y均为整数,x≥5,且y=$\frac{30}{x}$,
∴x可以为5,6,10,15,30.
∵2x+y≤20,即2x+$\frac{30}{x}$≤20,
∴x可以为5,6.共有两种围建方案.方案一:AB的长为5m,BC的长为6m;方案二:AB的长为6m,BC的长为5m.