《2025年5年中考3年模拟九年级数学上册北师大版》

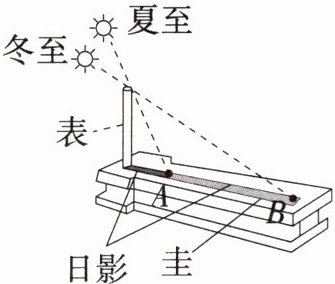
9.「2025山东济南历下期中,」如图,圭表是古代一种以度量日影长度来确定时间的仪器,垂直于地面的直杆叫“表”,水平放置于地面上刻有刻度以测量影长的标尺叫“圭”.当正午太阳光照射在表上时,日影便会投影在圭面上,冬至日影最长,夏至日影最短.冬至线与夏至线分别与圭面交于点B,A,若AB的长为3.5m,则表高为 ( )
(参考数据:冬至时,$\frac{表高}{影长}= 0.5$;夏至时,$\frac{表高}{影长}= 3$)


A.2.1m
B.2.4m
C.5.6m
D.5.8m

答案：
A　如图, 　　　　　　 设表高CD=x m.根据题意可得BC=2x m,AC=$\frac{1}{3}x$ m,
∵AB=3.5 m,
∴2x - $\frac{1}{3}x$=3.5,解得x=2.1.
∴表高CD=2.1 m.故选A.

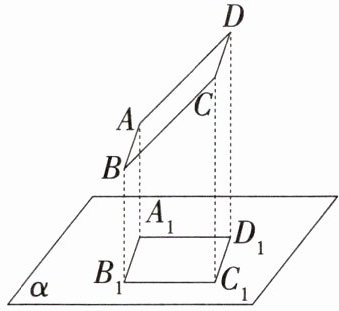
10.「2024山东烟台龙口期末,」如图,正方形纸板ABCD在投影面α上的正投影为四边形$A_1B_1C_1D_1,$其中边AB,CD与投影面平行,AD,BC与投影面不平行,若正方形ABCD的边长为4厘米$,∠BCC_1= 45°,$求四边形$A_1B_1C_1D_1$的面积.

答案：
解析　如图,过B点作BH⊥CC₁于H. 　　　　　　
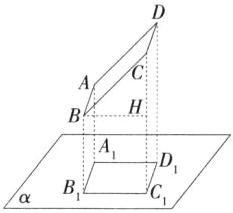
∵∠BCC₁=45°,
∴△BCH是等腰直角三角形,易知BH=$\frac{\sqrt{2}}{2}BC=\frac{\sqrt{2}}{2}×4 = 2\sqrt{2}$(厘米),
∵正方形纸板ABCD在投影面α上的正投影为四边形A₁B₁C₁D₁,
∴B₁C₁=BH=2$\sqrt{2}$厘米,C₁D₁=CD=4厘米,四边形A₁B₁C₁D₁为矩形,
∴四边形A₁B₁C₁D₁的面积=2$\sqrt{2}×4 = 8\sqrt{2}$(平方厘米).

11.在“测量物体的高度”活动中,某数学兴趣小组的3名同学选择测量学校里的3棵树的高度.在同一时刻的阳光下,他们分别做了以下工作:
小芳:测得一根长为1m的竹竿的影长为0.8m,甲树的影长为4m,如图①.
小华:发现乙树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上,如图②,墙壁上的影长为1.2m,落在地面上的影长为2.4m.
小丽:测量的丙树的影子除落在地面上外,还有一部分落在教学楼的第一级台阶上,如图③,测得第一级台阶上的影长为0.2m,第一级台阶的高为0.3m,落在地面上的影长为4.4m.
(1)甲树的高度为5m.
(2)求乙树的高度.
设2.4 m的影长对应的垂直高度为y m，根据题意得$\frac{1}{0.8}=\frac{y}{2.4}$，解得y=3，∴乙树的高度为3 + 1.2 = 4.2(m)。
(3)求丙树的高度.
设台阶上0.2 m的影长对应的垂直高度为h m，则$\frac{1}{0.8}=\frac{h}{0.2}$，解得h=0.25，设4.4 m的影长对应的垂直高度为w m，则$\frac{1}{0.8}=\frac{w}{4.4}$，解得w=5.5，∴丙树的高度为0.25 + 5.5 + 0.3 = 6.05(m)。

答案： 解析　
(1)设甲树的高度为x m,则$\frac{1}{0.8}=\frac{x}{4}$,解得x=5,故答案为5.
(2)设2.4 m的影长对应的垂直高度为y m,根据题意得$\frac{1}{0.8}=\frac{y}{2.4}$,解得y=3,
∴乙树的高度为3 + 1.2 = 4.2(m).
(3)设台阶上0.2 m的影长对应的垂直高度为h m,则$\frac{1}{0.8}=\frac{h}{0.2}$,解得h=0.25,设4.4 m的影长对应的垂直高度为w m,则$\frac{1}{0.8}=\frac{w}{4.4}$,解得w=5.5,
∴丙树的高度为0.25 + 5.5 + 0.3 = 6.05(m).