《2025年5年中考3年模拟九年级数学上册北师大版》

1.下列投影中,属于平行投影的是 (B)
A.晚上路灯下小孩的影子
B.阳光下沙滩上人的影子
C.汽车灯光照射下行人的影子
D.皮影戏中的影子

答案： B　太阳光线所形成的投影是平行投影，故选B.

2.「2025河南平顶山鲁山期末」在下列四幅图形中,能表示两棵小树在同一时刻阳光下的影子的是 (D)

答案： D　选项A,B,两棵小树的影子的方向相反,不可能为同一时刻阳光下的影子，所以A,B选项错误;选项C中较高的小树影子短，较矮的小树影子长，不符合在同一时刻阳光下,树高与影子成正比，所以C 选项错误;选项D,在同一时刻阳光下，影子方向相同,树高与影长成正比，所以D选项正确.故选D.

3.把一个正六棱柱按如图所示的方式摆放,光线由上向下照射此正六棱柱时得到的正投影是 (A)

答案： A　把一个正六棱柱按题图中的方式摆放，光线由上向下照射此正六棱柱时得到的正投影是正六边形.故选A.

4.「2025宁夏银川外国语实验学校月考」下面四幅图是两个物体不同时刻在太阳光下的影子,按照一天中时间的先后顺序正确的是 (C)
A.①→②→③→④
B.④→②→③→①
C.③→④→①→②
D.①→③→②→④

答案： C　不同时刻物体在太阳光下的影子的长短、方向改变的规律:就北半球而言，从早晨到傍晚物体的影子的指向是:西→西北→北→东北→东,影长由长变短，再变长.根据平行投影的特点和规律可知，按照一天中时间的先后顺序正确的是③→④→①→②.故选C.

5.小华拿一个矩形木框在阳光下玩,矩形木框在地面上形成的投影可能是②③④(填序号).

答案： 答案　②③④ 解析　矩形木框在地面上形成的投影应是平行四边形或一条线段，即相对的边平行或重合，故①不可能，即不会是梯形.故答案为②③④.

6.小红想利用阳光下的影长测量学校旗杆AB的高度.如图,某一时刻,他在地面上竖直立了一根2米长的标杆CD,测得其影长DE= 0.4米.
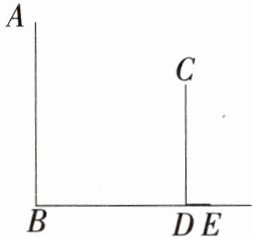
(1)请在图中画出此时旗杆AB在阳光下的投影BF.
(2)如果BF= 1.6米,求旗杆AB的高.

答案：
解析　
(1)连接CE,过A点作AF//CE交BD于F,则BF为所求,如图. 　　　　　　　　
(2)
∵AF//CE,
∴∠AFB=∠CED,又
∵∠ABF=∠CDE=90°,
∴△ABF∽△CDE,
∴$\frac{AB}{CD}=\frac{BF}{DE}$,即$\frac{AB}{2}=\frac{1.6}{0.4}$,
∴AB=8m. 答:旗杆AB的高为8米. 方法归纳　求平行投影中相关线段的长的方法：解决与平行投影有关的作图与计算问题，往往需要根据平行投影的性质画出投射线，得到相关的线段，从而根据同一时刻太阳光下，不同物体的高度比与其影长比相等，求得线段的长.

7.「2023山东枣庄中考,」如图,太阳光线平行照射在放置于地面的正六边形上,若∠1= 44°,则∠2的度数为 ( )


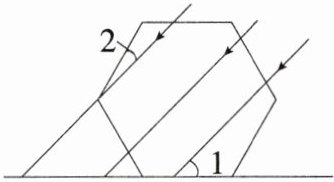
A.14°
B.16°
C.24°
D.26°

答案：
B　如图,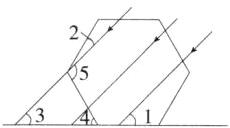 　　　　　　
∵正六边形的一个外角的度数为360°÷6=60°,
∴∠4=60°,正六边形的一个内角的度数为180°−60°=120°,即∠2+∠5=120°,
∵太阳光线是平行的，∠1=44°,
∴∠3=∠1=44°,
∴∠5=∠3+∠4=104°,
∴∠2=120°−∠5=16°.故选B.

8.「2024福建泉州期末,」甲、乙两人沿着如图所示的平行四边形空地边缘进行跑步比赛,两人同时从点B出发,沿着平行四边形边缘顺时针跑步,且甲的速度是乙的速度的2倍.当甲到达点E,乙到达点F时,甲、乙的影子(太阳光照射)刚好在同一条直线上,此时,点B处一根杆子的影子(太阳光照射)刚好在对角线BD上,则CE的长为 ( )


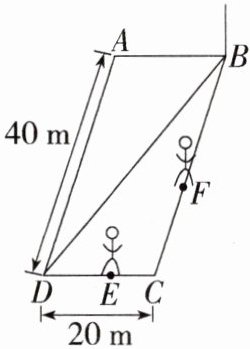
A.4m
B.8m
C.12m
D.16m

答案：
B　连接EF,如图, 　　　　　　　　　　　　　　 由题可知EF//BD,
∴△CEF∽△CDB,
∴$\frac{CE}{CD}=\frac{CF}{CB}$,
∵两人同时从点B出发，沿着平行四边形边缘顺时针跑步，且甲的速度是乙的速度的2倍,
∴BC+CE=2BF=40+CE,
∴BF=$\frac{1}{2}(40+CE)=20+\frac{1}{2}CE$,
∴CF=40 - 20 - $\frac{1}{2}CE$=20 - $\frac{1}{2}CE$,
∴$\frac{CE}{20}=\frac{20-\frac{1}{2}CE}{40}$,
∴CE=8m,故选B.