《2025年5年中考3年模拟九年级数学上册北师大版》

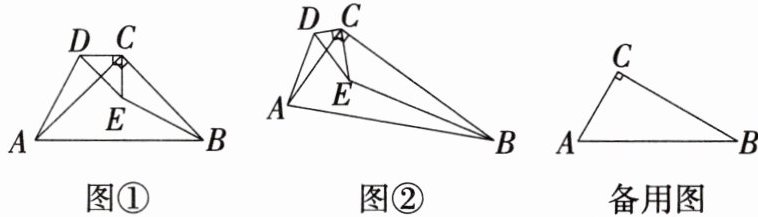
4.(1)如图①,已知A,E,B三点在同一条直线上,且$∠A= ∠B= ∠DEC= 90^{\circ }$,求证:$\triangle ADE\backsim \triangle BEC$.
(2)一位同学发现:如图②、图③,只要A,E,B三点在同一条直线上,且$∠A= ∠B= ∠DEC$,则(1)中的结论总成立.你同意吗?请在图②、图③中选择一个说明理由.

答案： 4.解析　
(1)证明:
∵∠A = ∠DEC = 90°,
∴∠DEA + ∠CEB = 90°,∠DEA + ∠D = 90°,
∴∠D = ∠CEB,又∠A = ∠B,
∴△ADE∽△BEC.
(2)同意.选择题图②说明理由:
∵∠A = ∠DEC,∠A + ∠D = ∠DEC + ∠CEB,
∴∠D = ∠CEB,又∠A = ∠B,
∴△ADE∽△BEC.
　(也可选题图③,证明过程相同)

5.如图,在$Rt\triangle ABC$中,$∠BAC= ∠ADC= 90^{\circ }$.若$AD= 3,BD= 2$,则CD的长为(C)
A.2
B.3
C.$\frac {9}{2}$
D.$\frac {4}{3}$

答案： 5.C
∵∠ADC = 90°,
∴∠ADB = 180° - ∠ADC = 90°,
∴∠B + ∠BAD = 90°.
∵∠BAC = 90°,
∴∠B + ∠C = 90°,
∴∠C = ∠BAD.
　又
∵∠ADC = ∠ADB,
∴△DAC∽△DBA,
∴$\frac{AD}{BD}$=$\frac{CD}{AD}$,
∵AD = 3,BD = 2,
∴$CD=\frac{9}{2}$.

6.[2025辽宁盘锦月考]【问题呈现】$\triangle CAB和\triangle CDE$都是直角三角形,$∠ACB= ∠DCE= 90^{\circ },CB= mCA,CE= mCD$,连接AD、BE,探究AD、BE的位置关系.
【问题探究】
(1)如图①,当$m= 1$时,判断AD、BE的位置关系,并说明理由.
(2)如图②,当$m= 2$时,AD、BE的位置关系为______.
【拓展应用】
(3)当$AB= 4\sqrt {7},DE= 4,∠ABC= ∠DEC= 30^{\circ }$时,将$\triangle CDE$绕点C旋转,使A,D,E三点恰好在同一直线上,直接写出BE的长.

答案：
6.解析　
(1)AD⊥BE.理由如下:
　如图①,延长BE交AD于点G,
　　　　　　　　
∵m = 1,
∴AC = BC,DC = EC,
∵∠DCE = ∠ACB = 90°,
∴∠DCA + ∠ACE = ∠ACE + ∠ECB = 90°,
∴∠DCA = ∠ECB,
∴△DCA≌△ECB(SAS),
∴∠DAC = ∠CBE,
∵∠GAB + ∠ABG = ∠DAC + ∠CAB + ∠ABG = ∠CBE + ∠CAB + ∠ABG = ∠CAB + ∠CBA = 180° - ∠ACB = 90°,
∴∠AGB = 180° - 90° = 90°,
∴BE⊥AD.
(2)BE⊥AD.
　详解:如图②,延长BE交AD于点G,
　　　　　　　　
∵m = 2,
∴CB = 2CA,CE = 2CD,
∴$\frac{DC}{CE}$=$\frac{AC}{BC}$=$\frac{1}{2}$,
∵∠DCE = ∠ACB = 90°,
∴∠DCA + ∠ACE = ∠ACE + ∠ECB = 90°,
∴∠DCA = ∠ECB,
∵$\frac{DC}{CE}$=$\frac{AC}{BC}$=$\frac{1}{2}$,
∴△DCA∽△ECB,
∴∠DAC = ∠CBE,
∵∠GAB + ∠ABG = ∠DAC + ∠CAB + ∠ABG
=∠CBE + ∠CAB + ∠ABG
=∠CAB + ∠CBA = 180° - ∠ACB = 90°,
∴∠AGB = 180° - 90° = 90°,
∴BE⊥AD.
(3)$BE = 6\sqrt{3}$或$4\sqrt{3}$.
详解:
∵在Rt△ABC中,∠ABC = 30°,
∴AB = AAC,根据勾股定理可得$BC=\sqrt{3}AC$,
∴$m=\frac{BC}{AC}=\sqrt{3}$,
∴$CE=\sqrt{3}CD$.
当点E在线段AD上时，连接BE,如图③.
设AE = x,则AD = AE + DE = x + AAE = x,则AD = AE + DE = x + 4,
∵∠DCE = ∠ACB,
∴∠DCE + ∠ACE = ∠ACB + ∠ACE,即∠DCA = ∠ECB,又
∵$\frac{DC}{CE}$=$\frac{AC}{BC}$,
∴△DCA∽△ECB,
∴$\frac{BE}{AD}$=$\frac{BC}{AC}=m=\sqrt{3}$,
∴$BE=\sqrt{3}AD=\sqrt{3}(x + 4)=\sqrt{3}x + 4\sqrt{3}$,
由
(2)可知BE⊥AD,
∴∠AEB = 90°,
根据勾股定理得$AE^2 + BE^2 = AB^2$,
即$x^2 + (\sqrt{3}x + 4\sqrt{3})^2 = (4\sqrt{7})^2$,
解得x = 2或x = - 8(舍去),
∴$BE=\sqrt{3}x + 4\sqrt{3}=6\sqrt{3}$.
　　　 　　
当点D在线段AE上时，连接BE,如图④.
设AD = y,则AE = AD + DE = y + 4,
易知△DCA∽△ECB,
∴$\frac{BE}{AD}$=$\frac{BC}{AC}=m=\sqrt{3}$,
∴$BE=\sqrt{3}AD=\sqrt{3}y$,
由
(2)可知BE⊥AD,
∴∠AEB = 90°,
根据勾股定理得$AE^2 + BE^2 = AB^2$,
即$(y + A)^2 + (\sqrt{3}y)^2 = (4\sqrt{7})^2$,
解得y = 4或y = - 6(舍去),此时$BE=\sqrt{3}y = 4\sqrt{3}$.
综上,$BE = 6\sqrt{3}$或$4\sqrt{3}$.