第73页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
11.「★☆☆」如图,在$\triangle ABC$中,点$D$,$E$,$F分别在边AB$,$AC$,$BC$上,连接$DE$,$EF$,已知四边形$BFED$是平行四边形,$\frac{DE}{BC}= \frac{1}{4}$.
(1)若$AB = 8$,求线段$AD$的长.
(2)若$\triangle ADE的面积为1$,求平行四边形$BFED$的面积.

(1)若$AB = 8$,求线段$AD$的长.
(2)若$\triangle ADE的面积为1$,求平行四边形$BFED$的面积.

答案:
(1)因为四边形BFED是平行四边形,所以DE//BC,所以△ADE∽△ABC.所以$\frac{AD}{AB}=\frac{DE}{BC}=\frac{1}{4}$.因为AB=8,所以AD=2.
(2)设△ABC的面积为S,△ADE的面积为$S_1$,△CEF的面积为$S_2$.因为$\frac{DE}{BC}=\frac{1}{4}$,所以$\frac{S_1}{S}=(\frac{DE}{BC})^2=\frac{1}{16}$.因为$S_1=1$,所以S=16.因为$\frac{DE}{BC}=\frac{AE}{AC}=\frac{1}{4}$,所以$\frac{CE}{CA}=\frac{3}{4}$.因为四边形BFED是平行四边形,所以EF//AB,所以△CEF∽△CAB.所以$\frac{S_2}{S}=(\frac{3}{4})^2=\frac{9}{16}$,所以$S_2=9$,所以平行四边形BFED的面积=$S-S_1-S_2=6$.
(1)因为四边形BFED是平行四边形,所以DE//BC,所以△ADE∽△ABC.所以$\frac{AD}{AB}=\frac{DE}{BC}=\frac{1}{4}$.因为AB=8,所以AD=2.
(2)设△ABC的面积为S,△ADE的面积为$S_1$,△CEF的面积为$S_2$.因为$\frac{DE}{BC}=\frac{1}{4}$,所以$\frac{S_1}{S}=(\frac{DE}{BC})^2=\frac{1}{16}$.因为$S_1=1$,所以S=16.因为$\frac{DE}{BC}=\frac{AE}{AC}=\frac{1}{4}$,所以$\frac{CE}{CA}=\frac{3}{4}$.因为四边形BFED是平行四边形,所以EF//AB,所以△CEF∽△CAB.所以$\frac{S_2}{S}=(\frac{3}{4})^2=\frac{9}{16}$,所以$S_2=9$,所以平行四边形BFED的面积=$S-S_1-S_2=6$.
12.新推理能力 如图,有一边长为$5\mathrm{cm}的正方形ABCD和等腰三角形PQR$,$PQ = PR = 5\mathrm{cm}$,$QR = 8\mathrm{cm}$,点$B$、$C$、$Q$、$R$在同一条直线上,当$C$、$Q$两点重合时,等腰三角形$PQR以1\mathrm{cm}/s的速度沿直线l$按箭头所示方向开始匀速运动,$t\mathrm{s}后正方形ABCD与等腰三角形PQR重合部分的面积为S\mathrm{cm}^2$.
(1)当$t = 3$时,求$S$的值.
(2)当$t = 5$时,求$S$的值.

(1)当$t = 3$时,求$S$的值.
(2)当$t = 5$时,求$S$的值.

答案:
(1)过P作PE⊥QR于点E,如图.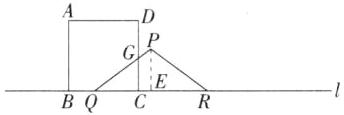
∵PQ=PR,
∴$QE=RE=\frac{1}{2}QR=4\ \text{cm}$.在Rt△PQE中,根据勾股定理,得$PE=\sqrt{PQ^2-QE^2}=\sqrt{5^2-4^2}=3\ \text{cm}$.当t=3时,QC=3 cm.设PQ交CD于点G.
∵PE//DC,
∴△QCG∽△QEP,
∴$\frac{S_{\triangle QCG}}{S_{\triangle QEP}}=(\frac{3}{4})^2=\frac{9}{16}$.
∵$S_{\triangle QEP}=\frac{1}{2}QE·PE=\frac{1}{2}×4×3=6(\text{cm}^2)$,
∴$S_{\triangle QCG}=\frac{9}{16}×6=\frac{27}{8}(\text{cm}^2)$,即$S=\frac{27}{8}$.
(2)当t=5时,点B与点Q重合,CR=3 cm,过P作PE⊥BC于点E,设PR与DC交于点M,如图.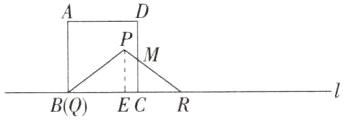
∵PE//DC,
∴△RCM∽△REP.同
(1)可求出$S_{\triangle RCM}=\frac{27}{8}\ \text{cm}^2$,
∴$S_{\text{四边形}PBCM}=S_{\triangle PQR}-S_{\triangle RCM}=2S_{\triangle QEP}-S_{\triangle RCM}=12-\frac{27}{8}=\frac{69}{8}(\text{cm}^2)$,即$S=\frac{69}{8}$.
(1)过P作PE⊥QR于点E,如图.

∵PQ=PR,
∴$QE=RE=\frac{1}{2}QR=4\ \text{cm}$.在Rt△PQE中,根据勾股定理,得$PE=\sqrt{PQ^2-QE^2}=\sqrt{5^2-4^2}=3\ \text{cm}$.当t=3时,QC=3 cm.设PQ交CD于点G.
∵PE//DC,
∴△QCG∽△QEP,
∴$\frac{S_{\triangle QCG}}{S_{\triangle QEP}}=(\frac{3}{4})^2=\frac{9}{16}$.
∵$S_{\triangle QEP}=\frac{1}{2}QE·PE=\frac{1}{2}×4×3=6(\text{cm}^2)$,
∴$S_{\triangle QCG}=\frac{9}{16}×6=\frac{27}{8}(\text{cm}^2)$,即$S=\frac{27}{8}$.
(2)当t=5时,点B与点Q重合,CR=3 cm,过P作PE⊥BC于点E,设PR与DC交于点M,如图.

∵PE//DC,
∴△RCM∽△REP.同
(1)可求出$S_{\triangle RCM}=\frac{27}{8}\ \text{cm}^2$,
∴$S_{\text{四边形}PBCM}=S_{\triangle PQR}-S_{\triangle RCM}=2S_{\triangle QEP}-S_{\triangle RCM}=12-\frac{27}{8}=\frac{69}{8}(\text{cm}^2)$,即$S=\frac{69}{8}$.
13.新应用意识 「2025山西长治壶关期中」阅读材料:三角形的三条中线必交于一点,这个交点称为三角形的重心.

(1)特例感知:如图a,已知边长为$2的等边\triangle ABC的重心为点O$,求$\triangle OBC与\triangle ABC$的面积.
(2)性质探究:如图b,已知$\triangle ABC的重心为点O$,请判断$\frac{OD}{OA}$、$\frac{S_{\triangle OBC}}{S_{\triangle ABC}}$是否都为定值?如果是,分别求出这两个定值;如果不是,请说明理由.
(3)性质应用:如图c,在正方形$ABCD$中,点$E是CD$的中点,连接$BE交对角线AC于点M$.
①若正方形$ABCD的边长为4$,求$EM$的长度;
②若$S_{\triangle CME}= 1$,求正方形$ABCD$的面积.

(1)特例感知:如图a,已知边长为$2的等边\triangle ABC的重心为点O$,求$\triangle OBC与\triangle ABC$的面积.
(2)性质探究:如图b,已知$\triangle ABC的重心为点O$,请判断$\frac{OD}{OA}$、$\frac{S_{\triangle OBC}}{S_{\triangle ABC}}$是否都为定值?如果是,分别求出这两个定值;如果不是,请说明理由.
(3)性质应用:如图c,在正方形$ABCD$中,点$E是CD$的中点,连接$BE交对角线AC于点M$.
①若正方形$ABCD的边长为4$,求$EM$的长度;
②若$S_{\triangle CME}= 1$,求正方形$ABCD$的面积.
答案:
(1)连接DE,如图1,
∵点O是△ABC的重心,
∴AD,BE分别是BC,AC边上的中线,
∴D,E分别为BC,AC的中点,
∴DE为△ABC的中位线,
∴DE//AB,$DE=\frac{1}{2}AB$,
∴△ODE∽△OAB,
∴$\frac{OD}{OA}=\frac{DE}{AB}=\frac{1}{2}$,
∵AB=2,BD=1,∠ADB=90°,
∴$AD=\sqrt{3}$,
∴$OD=\frac{\sqrt{3}}{3}$,$S_{\triangle ABC}=\frac{BC·AD}{2}=\frac{2×\sqrt{3}}{2}=\sqrt{3}$,
∴$S_{\triangle OBC}=\frac{BC·OD}{2}=\frac{2×\frac{\sqrt{3}}{3}}{2}=\frac{\sqrt{3}}{3}$.

(2)都是定值.由
(1)同理可得$\frac{OD}{OA}=\frac{1}{2}$,是定值.
∵$\frac{OD}{OA}=\frac{1}{2}$,
∴$\frac{OD}{AD}=\frac{1}{3}$,
∴$\frac{S_{\triangle OBD}}{S_{\triangle ABD}}=\frac{1}{3}$,同理可得$\frac{S_{\triangle ODC}}{S_{\triangle ADC}}=\frac{1}{3}$,
∵$S_{\triangle OBC}=S_{\triangle OBD}+S_{\triangle ODC}$,$S_{\triangle ABC}=S_{\triangle ABD}+S_{\triangle ADC}$,
∴$\frac{S_{\triangle OBC}}{S_{\triangle ABC}}=\frac{1}{3}$,是定值.
(3)①如图2,连接BD交AC于点O,
∵点O为BD的中点,点E为CD的中点,
∴点M是△BCD的重心,
∴$\frac{EM}{BE}=\frac{1}{3}$,
∵E为CD的中点,
∴$CE=\frac{1}{2}CD=2$,
∴$BE=\sqrt{BC^2+CE^2}=2\sqrt{5}$,
∴$EM=\frac{1}{3}BE=\frac{2\sqrt{5}}{3}$. ②
∵$S_{\triangle CME}=1$,且$\frac{ME}{BM}=\frac{1}{2}$,
∴$S_{\triangle BMC}=2$,
∵$\frac{ME}{BM}=\frac{1}{2}$,
∴$\frac{S_{\triangle CME}}{S_{\triangle AMB}}=(\frac{ME}{BM})^2=\frac{1}{4}$,
∴$S_{\triangle AMB}=4$,
∴$S_{\triangle ABC}=S_{\triangle BMC}+S_{\triangle ABM}=2+4=6$,又$S_{\triangle ADC}=S_{\triangle ABC}$,
∴$S_{\triangle ADC}=6$,
∴正方形ABCD的面积为6+6=12.
(1)连接DE,如图1,
∵点O是△ABC的重心,
∴AD,BE分别是BC,AC边上的中线,
∴D,E分别为BC,AC的中点,
∴DE为△ABC的中位线,
∴DE//AB,$DE=\frac{1}{2}AB$,
∴△ODE∽△OAB,
∴$\frac{OD}{OA}=\frac{DE}{AB}=\frac{1}{2}$,
∵AB=2,BD=1,∠ADB=90°,
∴$AD=\sqrt{3}$,
∴$OD=\frac{\sqrt{3}}{3}$,$S_{\triangle ABC}=\frac{BC·AD}{2}=\frac{2×\sqrt{3}}{2}=\sqrt{3}$,
∴$S_{\triangle OBC}=\frac{BC·OD}{2}=\frac{2×\frac{\sqrt{3}}{3}}{2}=\frac{\sqrt{3}}{3}$.


(2)都是定值.由
(1)同理可得$\frac{OD}{OA}=\frac{1}{2}$,是定值.
∵$\frac{OD}{OA}=\frac{1}{2}$,
∴$\frac{OD}{AD}=\frac{1}{3}$,
∴$\frac{S_{\triangle OBD}}{S_{\triangle ABD}}=\frac{1}{3}$,同理可得$\frac{S_{\triangle ODC}}{S_{\triangle ADC}}=\frac{1}{3}$,
∵$S_{\triangle OBC}=S_{\triangle OBD}+S_{\triangle ODC}$,$S_{\triangle ABC}=S_{\triangle ABD}+S_{\triangle ADC}$,
∴$\frac{S_{\triangle OBC}}{S_{\triangle ABC}}=\frac{1}{3}$,是定值.
(3)①如图2,连接BD交AC于点O,
∵点O为BD的中点,点E为CD的中点,
∴点M是△BCD的重心,
∴$\frac{EM}{BE}=\frac{1}{3}$,
∵E为CD的中点,
∴$CE=\frac{1}{2}CD=2$,
∴$BE=\sqrt{BC^2+CE^2}=2\sqrt{5}$,
∴$EM=\frac{1}{3}BE=\frac{2\sqrt{5}}{3}$. ②
∵$S_{\triangle CME}=1$,且$\frac{ME}{BM}=\frac{1}{2}$,
∴$S_{\triangle BMC}=2$,
∵$\frac{ME}{BM}=\frac{1}{2}$,
∴$\frac{S_{\triangle CME}}{S_{\triangle AMB}}=(\frac{ME}{BM})^2=\frac{1}{4}$,
∴$S_{\triangle AMB}=4$,
∴$S_{\triangle ABC}=S_{\triangle BMC}+S_{\triangle ABM}=2+4=6$,又$S_{\triangle ADC}=S_{\triangle ABC}$,
∴$S_{\triangle ADC}=6$,
∴正方形ABCD的面积为6+6=12.
查看更多完整答案,请扫码查看


