《2025年5年中考3年模拟九年级数学上册北师大版》

1.「2024重庆中考B卷」若两个相似三角形的相似比为$1:4$,则这两个三角形面积的比是(D)
A.$1:2$
B.$1:4$
C.$1:8$
D.$1:16$

答案： 根据相似三角形的面积之比等于相似比的平方知,若两个相似三角形的相似比为1∶4,则这两个三角形面积的比是1∶16,故选D.

2.「2025河北武邑期中」若$\triangle ABC\backsim\triangle DEF$,$AB = 1$,$DE = 2$,则$\triangle ABC与\triangle DEF$的周长比是(A)
A.$1:2$
B.$1:3$
C.$2:3$
D.$3:2$

答案：
∵△ABC∽△DEF,
∴△ABC与△DEF的相似比为$\frac{AB}{DE}=\frac{1}{2}$,即相似比为1∶2.根据相似三角形的周长比等于相似比可得△ABC与△DEF的周长比是1∶2.故选A.

3.「2024河北石家庄模拟」如图所示,$\triangle ABC$中,$DE// BC$,若$AD:DB = 1:2$,则下列结论中正确的是(D)

A.$\frac{DE}{BC}= \frac{1}{2}$
B.$\frac{\triangle ADE的周长}{\triangle ABC的周长}= \frac{1}{2}$
C.$\frac{\triangle ADE的面积}{\triangle ABC的面积}= \frac{1}{3}$
D.$\frac{\triangle ADE的周长}{\triangle ABC的周长}= \frac{1}{3}$

答案：
∵DE//BC,
∴△ADE∽△ABC,
∵AD∶DB=1∶2,
∴AD∶AB=1∶3,
∴△ADE和△ABC的相似比为1∶3,
∵周长比等于相似比，面积比等于相似比的平方，
∴D中结论正确.故选D.

4.「2024云南中考」如图,$AB与CD交于点O$,且$AC// BD$.若$\frac{OA + OC + AC}{OB + OD + BD}= \frac{1}{2}$,则$\frac{AC}{BD}= $$\frac{1}{2}$.

答案： $\frac{1}{2}$ 解析
∵AC//BD,
∴△AOC∽△BOD,根据相似三角形的周长比等于相似比知$\frac{OA+OC+AC}{OB+OD+BD}=\frac{AC}{BD}$,
∵$\frac{OA+OC+AC}{OB+OD+BD}=\frac{1}{2}$,
∴$\frac{AC}{BD}=\frac{1}{2}$,故答案为$\frac{1}{2}$.

5.如图所示,平行四边形$ABCD$中,$E是BC$边上一点,且$BE = EC$,$BD$,$AE相交于F$点.
(1)求$\triangle BEF与\triangle AFD$的周长之比.
(2)若$S_{\triangle BEF}= 6\mathrm{cm}^2$,求$S_{\triangle AFD}$.

周长比、面积比的性质 答案D48

答案：
(1)
∵在平行四边形ABCD中,AD//BC,
∴△BEF∽△DAF.
∵AD=BC,BE=EC,
∴BE=$\frac{1}{2}$BC=$\frac{1}{2}$AD,
∴$\frac{BE}{AD}=\frac{1}{2}$,
∴△BEF与△AFD的周长之比为1∶2.
(2)由
(1)可知△BEF∽△DAF,且相似比为$\frac{1}{2}$,
∴$\frac{S_{\triangle BEF}}{S_{\triangle AFD}}=(\frac{1}{2})^2$,
∴$S_{\triangle AFD}=4S_{\triangle BEF}=4×6=24(\text{cm}^2)$.

6.如图,在四边形$ABCD$中,$E$,$F$,$G分别是BA$,$BD$,$BC$上的点,$EF// AD$,$FG// DC$,且$\frac{AE}{BE}= \frac{1}{2}$,则四边形$ABCD和四边形EBGF$的周长之比为(B)
A.$4:3$
B.$3:2$
C.$4:1$
D.$2:1$

答案： 因为$\frac{AE}{BE}=\frac{1}{2}$,所以$\frac{AB}{BE}=\frac{3}{2}$.因为EF//AD,所以△BEF∽△BAD,所以$\frac{BE}{AB}=\frac{EF}{AD}=\frac{BF}{BD}$.因为FG//CD,所以△BFG∽△BDC,所以$\frac{BF}{BD}=\frac{FG}{CD}=\frac{BG}{BC}$,所以$\frac{BE}{BA}=\frac{EF}{AD}=\frac{FG}{CD}=\frac{BG}{BC}$.由EF//AD,FG//CD可知∠A=∠BEF,∠C=∠FGB,∠ADB=∠EFB,∠BDC=∠BFG,所以∠ADC=∠EFG,又∠ABC=∠EBG,所以四边形ABCD∽四边形EBGF,所以$\frac{\text{四边形}ABCD\text{的周长}}{\text{四边形}EBGF\text{的周长}}=\frac{AB}{EB}=\frac{3}{2}$. 故选B.

7.「2024陕西咸阳武功期末」四边形$ABCD\backsim四边形A'B'C'D'$,$AB:A'B' = 1:4$,若四边形$ABCD的周长为3$,则四边形$A'B'C'D'$的周长为12.

答案： 12 解析
∵四边形ABCD∽四边形A'B'C'D',$\frac{AB}{A'B'}=\frac{1}{4}$,
∴$\frac{\text{四边形}ABCD\text{的周长}}{\text{四边形}A'B'C'D'\text{的周长}}=\frac{1}{4}$,
∵四边形ABCD的周长为3,
∴四边形A'B'C'D'的周长为12.

8.「2025陕西西安新城期中,★☆☆」如图,在正方形网格中,$A$,$B$,$C$,$D$是网格线的交点,$AC与BD相交于点O$,则$\triangle ABO的周长与\triangle CDO$的周长之比为(A)

A.$1:2$
B.$\sqrt{2}:2$
C.$1:4$
D.$\sqrt{2}:4$

答案： 设题图中每个小正方形的边长为1,易知$AB=\sqrt{2}$,$CD=2\sqrt{2}$,AB//CD,
∴△AOB∽△COD,
∴△ABO的周长∶△CDO的周长=AB∶CD=1∶2.故选A.

9.「2025山东枣庄市中期中,★☆☆」如图,$\triangle ABC\backsim\triangle ADE$,$S_{\triangle ABC}:S_{四边形BDEC}= 1:2$,$BC= \sqrt{2}$,则$DE$的长为(A)
A.$\sqrt{6}$
B.$2\sqrt{2}$
C.$3\sqrt{2}$
D.$6$

答案：
∵$S_{\triangle ABC}:S_{\text{四边形}BDEC}=1:2$,
∴$S_{\triangle ABC}:S_{\triangle ADE}=1:3$,
∵△ABC∽△ADE,
∴$\frac{BC}{DE}=\sqrt{\frac{1}{3}}$,
∵$BC=\sqrt{2}$,
∴$DE=\sqrt{6}$.故选A.

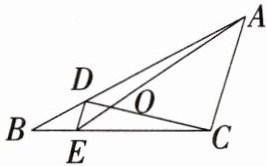
10.「2025四川威远新场中学期中,★☆☆」如图,$D$、$E分别是\triangle ABC的边AB$、$BC$上的点,且$DE// AC$,$AE$、$CD相交于点O$,若$S_{\triangle DOE}:S_{\triangle COA}= 4:49$,则$\frac{S_{\triangle BDE}}{S_{\triangle CDE}}$的值为( B )

A.$\frac{2}{3}$
B.$\frac{2}{5}$
C.$\frac{1}{3}$
D.$\frac{2}{25}$

答案：
∵D、E分别是△ABC的边AB、BC上的点,且DE//AC,
∴△DOE∽△COA,△DBE∽△ABC,
∵$S_{\triangle DOE}:S_{\triangle COA}=4:49$,
∴$\frac{DE}{AC}=\frac{2}{7}$,
∴$\frac{BE}{BC}=\frac{DE}{AC}=\frac{2}{7}$,
∴$\frac{BE}{EC}=\frac{2}{5}$,
∴$\frac{S_{\triangle BDE}}{S_{\triangle CDE}}=\frac{2}{5}$,故选B.