第70页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. 学科教材变式 特色P107T1 「2025河北张家口桥西期中」已知$\triangle ABC \backsim \triangle A'B'C'$,$BD和B'D'$是它们的对应角平分线,若$\frac {AC}{A'C'}= \frac {2}{3}$,$BD = 4$,则$B'D'= $
A.2
B.3
C.6
D.9
C
A.2
B.3
C.6
D.9
答案:
C
∵△ABC∽△A'B'C',BD和B'D'是它们的对应角平分线,
∴AC:A'C'=BD:B'D'。
∵$\frac{AC}{A'C'}=\frac{2}{3}$,BD = 4,
∴B'D' = 6,故选C。
∵△ABC∽△A'B'C',BD和B'D'是它们的对应角平分线,
∴AC:A'C'=BD:B'D'。
∵$\frac{AC}{A'C'}=\frac{2}{3}$,BD = 4,
∴B'D' = 6,故选C。
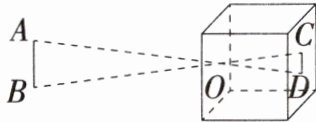
2. 跨物理 小孔成像 学科教材变式 素养P108习题T2 「2025河南南阳期中」为了证明光沿直线传播这一性质,大约在二千四百年前,我国杰出的科学家墨翟和他的学生做了世界上第一个小孔成像的实验,解释了小孔成倒像的原理.如图所示的是小孔成像原理的示意图,$AB$为蜡烛,$CD为蜡烛AB$在暗盒中所成的像,若$6 cm长的蜡烛AB在暗盒中所成的像CD的长是1 cm$,$AB与小孔O之间的距离为18 cm$,则小孔$O到像CD$的距离为(
A.$1 cm$
B.$2 cm$
C.$3 cm$
D.$4 cm$
C
)
A.$1 cm$
B.$2 cm$
C.$3 cm$
D.$4 cm$
答案:
C 设小孔O到像CD的距离为h cm,由题意可知△ABO与△CDO相似,
∵6 cm长的蜡烛AB在暗盒中所成的像CD的长是1 cm,
∴$\frac{18}{h}=\frac{6}{1}$,
∴h = 3。故选C。
∵6 cm长的蜡烛AB在暗盒中所成的像CD的长是1 cm,
∴$\frac{18}{h}=\frac{6}{1}$,
∴h = 3。故选C。
3. 「2025北京顺义三中期中」图1是可折叠的熨衣架的实物图,图2是它的侧面示意图,$AD与CB相交于点O$,$AB // CD$,根据图2中的数据可得$x$的值为(
A.0.4
B.0.35
C.0.3
D.0.6
A
)A.0.4
B.0.35
C.0.3
D.0.6
答案:
A
∵AB//CD,
∴△COD∽△BOA,
∴$\frac{CD}{BA}=\frac{x}{0.5}$,
∵$\frac{0.8}{1}=\frac{x}{0.5}$,
∴x = 0.4,故选A。
∵AB//CD,
∴△COD∽△BOA,
∴$\frac{CD}{BA}=\frac{x}{0.5}$,
∵$\frac{0.8}{1}=\frac{x}{0.5}$,
∴x = 0.4,故选A。
4. 「2025上海金山期中」如果两个相似三角形对应边上的高之比是$4:9$,那么它们的对应中线之比等于
4:9
.
答案:
答案 4:9 解析
∵两个相似三角形对应边上的高之比是4:9,
∴这两个相似三角形的相似比为4:9,
∴它们的对应中线之比等于4:9。故答案为4:9。
∵两个相似三角形对应边上的高之比是4:9,
∴这两个相似三角形的相似比为4:9,
∴它们的对应中线之比等于4:9。故答案为4:9。
5. 新考向 尺规作图 求证:相似三角形对应边上的中线之比等于相似比.
要求:
(1)根据给出的$\triangle ABC与∠A'(∠A' = ∠A)$,以$A'B'$为一边,在给出的图形上用尺规作出$\triangle A'B'C'$,使得$\triangle A'B'C' \backsim \triangle ABC$,不写作法,保留作图痕迹.
(2)在已有的图形上画出一组对应中线,并据此写出已知、求证和证明过程.
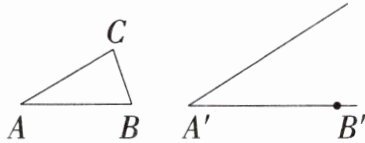
要求:
(1)根据给出的$\triangle ABC与∠A'(∠A' = ∠A)$,以$A'B'$为一边,在给出的图形上用尺规作出$\triangle A'B'C'$,使得$\triangle A'B'C' \backsim \triangle ABC$,不写作法,保留作图痕迹.
(2)在已有的图形上画出一组对应中线,并据此写出已知、求证和证明过程.
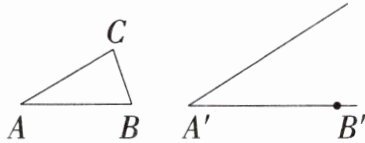
答案:
解析
(1)如图所示,△A'B'C'即为所求。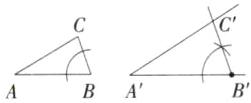
(2)(答案不唯一)已知:如图,△ABC∽△A'B'C',$\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{A'C'}{AC}=k$,D是AB的中点,D'是A'B'的中点。求证:$\frac{C'D'}{CD}=k$。 证明:
证明:
∵D是AB的中点,D'是A'B'的中点,
∴AD = $\frac{1}{2}$AB,A'D' = $\frac{1}{2}$A'B',
∴$\frac{A'D'}{AD}=\frac{\frac{1}{2}A'B'}{\frac{1}{2}AB}=\frac{A'B'}{AB}$。
∵△ABC∽△A'B'C',
∴$\frac{A'B'}{AB}=\frac{A'C'}{AC}$,∠A' = ∠A,
∴$\frac{A'D'}{AD}=\frac{A'C'}{AC}$,
∴△A'C'D'∽△ACD,
∴$\frac{C'D'}{CD}=\frac{A'C'}{AC}=k$。
解析
(1)如图所示,△A'B'C'即为所求。

(2)(答案不唯一)已知:如图,△ABC∽△A'B'C',$\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{A'C'}{AC}=k$,D是AB的中点,D'是A'B'的中点。求证:$\frac{C'D'}{CD}=k$。
 证明:
证明:∵D是AB的中点,D'是A'B'的中点,
∴AD = $\frac{1}{2}$AB,A'D' = $\frac{1}{2}$A'B',
∴$\frac{A'D'}{AD}=\frac{\frac{1}{2}A'B'}{\frac{1}{2}AB}=\frac{A'B'}{AB}$。
∵△ABC∽△A'B'C',
∴$\frac{A'B'}{AB}=\frac{A'C'}{AC}$,∠A' = ∠A,
∴$\frac{A'D'}{AD}=\frac{A'C'}{AC}$,
∴△A'C'D'∽△ACD,
∴$\frac{C'D'}{CD}=\frac{A'C'}{AC}=k$。
6. 如图,$\triangle ABC \backsim \triangle A'B'C'$,$BE$,$B'E'分别是\triangle ABC$,$\triangle A'B'C'$的角平分线,$D$,$D'分别是BC$,$B'C'$的三等分点,且$CD = 2BD$,$C'D' = 2B'D'$,连接$AD$,$A'D'$.求证:$\frac {AD}{A'D'}= \frac {BE}{B'E'}$.


答案:
证明
∵△ABC∽△A'B'C',BE,B'E'分别是△ABC,△A'B'C'的角平分线,
∴$\frac{BE}{B'E'}=\frac{AB}{A'B'}=\frac{BC}{B'C'}$,∠ABD = ∠A'B'D'。
∵CD = 2BD,C'D' = 2B'D',
∴BD = $\frac{1}{3}$BC,B'D' = $\frac{1}{3}$B'C',
∴$\frac{AB}{A'B'}=\frac{BD}{B'D'}$。
∵∠ABD = ∠A'B'D',
∴△ABD∽△A'B'D',
∴$\frac{AD}{A'D'}=\frac{AB}{A'B'}$,
∴$\frac{AD}{A'D'}=\frac{BE}{B'E'}$。
∵△ABC∽△A'B'C',BE,B'E'分别是△ABC,△A'B'C'的角平分线,
∴$\frac{BE}{B'E'}=\frac{AB}{A'B'}=\frac{BC}{B'C'}$,∠ABD = ∠A'B'D'。
∵CD = 2BD,C'D' = 2B'D',
∴BD = $\frac{1}{3}$BC,B'D' = $\frac{1}{3}$B'C',
∴$\frac{AB}{A'B'}=\frac{BD}{B'D'}$。
∵∠ABD = ∠A'B'D',
∴△ABD∽△A'B'D',
∴$\frac{AD}{A'D'}=\frac{AB}{A'B'}$,
∴$\frac{AD}{A'D'}=\frac{BE}{B'E'}$。
查看更多完整答案,请扫码查看


