第69页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
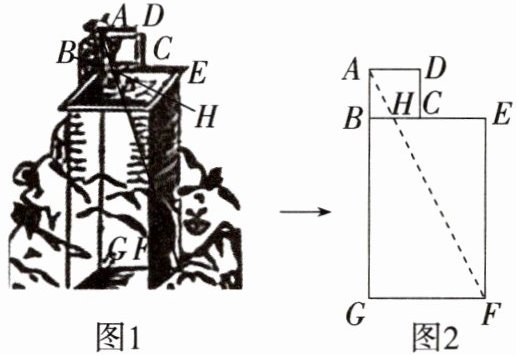
4.新考向数学文化「2025广西贵港桂平期中,」四分仪是一种十分古老的测量仪器.图1是古代测量员用四分仪测量一方井的深度的示意图,将四分仪置于方井上的边沿上,通过窥衡杆测望井底点F,窥衡杆与四分仪的一边BC交于点H.图2中,四分仪为正方形ABCD,方井为矩形BEFG.若测量员从四分仪中读得AB为1,BH为0.5,实地测得BE为2.5,则井深BG为(
A.4
B.5
C.6
D.7
A
)
A.4
B.5
C.6
D.7
答案:
4.A
∵四边形ABCD是正方形,
∴∠ABC=90°,
∵BE=2.5,BH=0.5,
∴HE=BE - BH=2.5 - 0.5=2,
∵四边形BEFG是矩形,
∴BG=EF,∠BEF=90°,
∴∠ABH=∠FEH=90°,
∵∠AHB=∠EHF,
∴△ABH∽△FEH,$\frac{AB}{EF}=\frac{BH}{EH}$,即$\frac{1}{EF}=\frac{0.5}{2}$,
∴EF=4,
∴BG=EF=4,故选A.
∵四边形ABCD是正方形,
∴∠ABC=90°,
∵BE=2.5,BH=0.5,
∴HE=BE - BH=2.5 - 0.5=2,
∵四边形BEFG是矩形,
∴BG=EF,∠BEF=90°,
∴∠ABH=∠FEH=90°,
∵∠AHB=∠EHF,
∴△ABH∽△FEH,$\frac{AB}{EF}=\frac{BH}{EH}$,即$\frac{1}{EF}=\frac{0.5}{2}$,
∴EF=4,
∴BG=EF=4,故选A.
5.「2025河南郑州四中月考,」操场上有一根竖直的旗杆AB,它的一部分影子(BC)落在水平地面上,另一部分影子(CD)落在墙壁上,经测量,墙壁上的影高为1.2m,地面上的影长为2.8m,同时测得一根高为2m的竹竿OM的影长ON= 1.4m,则旗杆的高度是( )

A.4.5m
B.104.7m
C.5.2m
D.5.7m

A.4.5m
B.104.7m
C.5.2m
D.5.7m
答案:
5.C 如图,过点D作DE⊥AB于点E,

由题意可知,BE=CD=1.2 m,BC=DE=2.8 m,$\frac{OM}{ON}=\frac{AE}{DE}$,
∵OM=2 m,ON=1.4 m,$\frac{2}{1.4}=\frac{AB - 1.2}{2.8}$,解得AB=5.2 m,
∴旗杆的高度是5.2 m,故选C.
5.C 如图,过点D作DE⊥AB于点E,

由题意可知,BE=CD=1.2 m,BC=DE=2.8 m,$\frac{OM}{ON}=\frac{AE}{DE}$,
∵OM=2 m,ON=1.4 m,$\frac{2}{1.4}=\frac{AB - 1.2}{2.8}$,解得AB=5.2 m,
∴旗杆的高度是5.2 m,故选C.
6.新考向项目探究题「2024河南邓州期中,」下面是小明进行数学学科项目学习时,填写活动报告的部分内容.
项目主题:测量河流的宽度.
项目探究:河流宽度不能直接测量,需要借助一些工具,比如:镜子,标杆,皮尺,自制的直角三角形模板,……各组确定方案后,选择测量工具,画出测量示意图,并进行实地测量,得到具体数据,从而计算出河流的宽度.
项目成果:下表是小明进行交流展示时的部分测量方案及测量数据: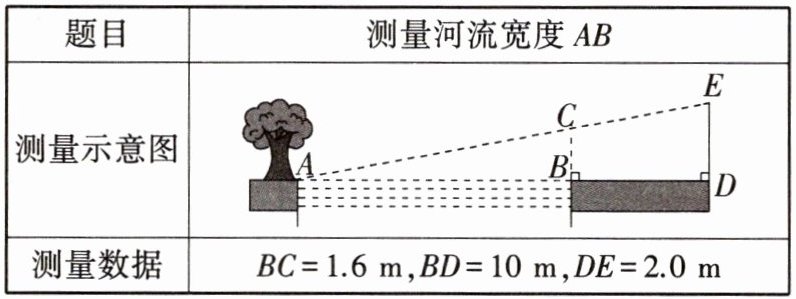
请你参与这个项目学习,并完成下列任务:
(1)任务一:请你借助小明的测量数据,计算河流的宽度AB.
(2)任务二:请你写出这个方案中求河流宽度时用到的数学知识:______(写出一条即可).
(3)任务三:请你设计一个与小明不同的测量方案,并画图简要说明.
项目主题:测量河流的宽度.
项目探究:河流宽度不能直接测量,需要借助一些工具,比如:镜子,标杆,皮尺,自制的直角三角形模板,……各组确定方案后,选择测量工具,画出测量示意图,并进行实地测量,得到具体数据,从而计算出河流的宽度.
项目成果:下表是小明进行交流展示时的部分测量方案及测量数据:

请你参与这个项目学习,并完成下列任务:
(1)任务一:请你借助小明的测量数据,计算河流的宽度AB.
(2)任务二:请你写出这个方案中求河流宽度时用到的数学知识:______(写出一条即可).
(3)任务三:请你设计一个与小明不同的测量方案,并画图简要说明.
答案:
6.解析
(1)由题意知,BC//DE,
∴△ABC∽△ADE.$\frac{AB}{AD}=\frac{BC}{DE}$,又BC=1.6 m,BD=10 m,DE=2.0 m,$\frac{AB}{AB + 10}=\frac{1.6}{2.0}$,解得AB=40 m.答:河流的宽度AB为40 m.
(2)相似三角形的对应边成比例(答案不唯一,合理即可).\\n
(3)(答案不唯一,合理即可)如图,在河对岸找一个参照物A,站在A的正对面B的位置,沿着河岸向东走一段距离,到达C处,在C处直立一竹竿,然后继续向东行走到D处,使得CD=BC,再沿着与河岸垂直的方向行走,当走到与A、C共线的位置时停下,位置记为E,这时DE的长等于河流的宽度.

6.解析
(1)由题意知,BC//DE,
∴△ABC∽△ADE.$\frac{AB}{AD}=\frac{BC}{DE}$,又BC=1.6 m,BD=10 m,DE=2.0 m,$\frac{AB}{AB + 10}=\frac{1.6}{2.0}$,解得AB=40 m.答:河流的宽度AB为40 m.
(2)相似三角形的对应边成比例(答案不唯一,合理即可).\\n
(3)(答案不唯一,合理即可)如图,在河对岸找一个参照物A,站在A的正对面B的位置,沿着河岸向东走一段距离,到达C处,在C处直立一竹竿,然后继续向东行走到D处,使得CD=BC,再沿着与河岸垂直的方向行走,当走到与A、C共线的位置时停下,位置记为E,这时DE的长等于河流的宽度.

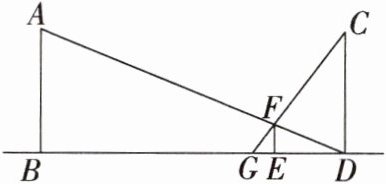
7.新课标应用意识如图,广场上有两盏高度相同的路灯A、C,相距20m,晚上身高为1.8m的张明站在两个路灯之间的E处,此时ED为张明在路灯A照射下的影子,GE为张明在路灯C照射下的影子,已知DG= 5m,求路灯的高度.

答案:
7.解析
∵AB⊥BD,EF⊥BD,
∴∠ABD=∠FED,
∵∠ADB=∠FDE,
∴△ABD∽△FED,$\frac{AB}{EF}=\frac{BD}{DE}$,设AB=CD=x m,DE=y m,$\frac{x}{1.8}=\frac{20}{y}$,同理:△CDG∽△FEG,$\frac{CD}{EF}=\frac{DG}{EG}$,$\frac{x}{1.8}=\frac{5}{5 - y}$,
∴$\frac{20}{y}=\frac{5}{5 - y}$,解得y=4,经检验,y=4是方程的解,由$\frac{x}{1.8}=\frac{20}{y}$得$\frac{x}{1.8}=\frac{20}{4}$,解得x=9.答:路灯的高度为9 m.
∵AB⊥BD,EF⊥BD,
∴∠ABD=∠FED,
∵∠ADB=∠FDE,
∴△ABD∽△FED,$\frac{AB}{EF}=\frac{BD}{DE}$,设AB=CD=x m,DE=y m,$\frac{x}{1.8}=\frac{20}{y}$,同理:△CDG∽△FEG,$\frac{CD}{EF}=\frac{DG}{EG}$,$\frac{x}{1.8}=\frac{5}{5 - y}$,
∴$\frac{20}{y}=\frac{5}{5 - y}$,解得y=4,经检验,y=4是方程的解,由$\frac{x}{1.8}=\frac{20}{y}$得$\frac{x}{1.8}=\frac{20}{4}$,解得x=9.答:路灯的高度为9 m.
查看更多完整答案,请扫码查看


