第67页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
7.「2024 山东济南槐荫期中」【问题背景】$\triangle ABC$中,$AB = AC$,$∠BAC = 90^{\circ}$,$P为BC$上的动点,现将一个含$45^{\circ}角的透明三角尺的45^{\circ}角的顶点落在点P$处,使三角尺绕点$P$旋转。
【用数学的眼光观察】(1)如图 1,当三角尺的两边分别交$AB$、$AC于点E$、$F$时,以下结论正确的是____。
①$\triangle BPE \cong \triangle CFP$;②$\triangle BPE \backsim \triangle CFP$;③$∠BEP = ∠CPF$;④$\frac{BE}{CP} = \frac{PE}{FP}$。
【用数学的思维思考】(2)将三角尺绕点$P$旋转到如图 2 所示的位置时,三角尺的两边分别交$BA$的延长线、边$AC于点E$、$F$,$\triangle BPE与\triangle CFP$相似吗?请说明理由。
【用数学的语言表达】(3)在(2)的条件下,动点$P$运动到什么位置时,$\triangle BPE \backsim \triangle PFE$?说明理由。
【用数学的眼光观察】(1)如图 1,当三角尺的两边分别交$AB$、$AC于点E$、$F$时,以下结论正确的是____。
①$\triangle BPE \cong \triangle CFP$;②$\triangle BPE \backsim \triangle CFP$;③$∠BEP = ∠CPF$;④$\frac{BE}{CP} = \frac{PE}{FP}$。
【用数学的思维思考】(2)将三角尺绕点$P$旋转到如图 2 所示的位置时,三角尺的两边分别交$BA$的延长线、边$AC于点E$、$F$,$\triangle BPE与\triangle CFP$相似吗?请说明理由。
【用数学的语言表达】(3)在(2)的条件下,动点$P$运动到什么位置时,$\triangle BPE \backsim \triangle PFE$?说明理由。
答案:
解析
(1)
∵ AB=AC,∠BAC=90°,
∴ ∠B=∠C=45°,
∴ ∠BEP=180°-45°-∠BPE=135°-∠BPE,
∵ ∠EPF=45°,
∴ ∠CPF=180°-45°-∠BPE=135°-∠BPE,
∴ ∠BEP=∠CPF,
∴ △BPE∽△CFP,
∴ $\frac{BE}{CP}=\frac{PE}{FP}$,但△BPE 与△CFP 不一定全等.故①错误,②③④正确,故答案为②③④.
(2)△BPE∽△CFP.理由:
∵ AB=AC,∠BAC=90°,
∴ ∠B=∠C=45°,
∴ ∠BEP=180°-45°-∠BPE=135°-∠BPE,
∵ ∠EPF=45°,
∴ ∠CPF=180°-45°-∠BPE=135°-∠BPE,
∴ ∠BEP=∠CPF,
∴ △BPE∽△CFP.
(3)当点 P 为 BC 的中点时,△BPE∽△PFE.理由:如图,连接 EF,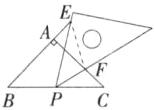
∵ △BPE∽△CFP,
∴ $\frac{BE}{CP}=\frac{PE}{FP}$,
∵ P 为 BC 的中点,
∴ CP=PB,
∴ $\frac{BE}{PB}=\frac{PE}{FP}$,
∴ $\frac{BE}{PE}=\frac{PB}{FP}$,
∵ ∠B=∠EPF,
∴ △BPE∽△PFE.
解析
(1)
∵ AB=AC,∠BAC=90°,
∴ ∠B=∠C=45°,
∴ ∠BEP=180°-45°-∠BPE=135°-∠BPE,
∵ ∠EPF=45°,
∴ ∠CPF=180°-45°-∠BPE=135°-∠BPE,
∴ ∠BEP=∠CPF,
∴ △BPE∽△CFP,
∴ $\frac{BE}{CP}=\frac{PE}{FP}$,但△BPE 与△CFP 不一定全等.故①错误,②③④正确,故答案为②③④.
(2)△BPE∽△CFP.理由:
∵ AB=AC,∠BAC=90°,
∴ ∠B=∠C=45°,
∴ ∠BEP=180°-45°-∠BPE=135°-∠BPE,
∵ ∠EPF=45°,
∴ ∠CPF=180°-45°-∠BPE=135°-∠BPE,
∴ ∠BEP=∠CPF,
∴ △BPE∽△CFP.
(3)当点 P 为 BC 的中点时,△BPE∽△PFE.理由:如图,连接 EF,

∵ △BPE∽△CFP,
∴ $\frac{BE}{CP}=\frac{PE}{FP}$,
∵ P 为 BC 的中点,
∴ CP=PB,
∴ $\frac{BE}{PB}=\frac{PE}{FP}$,
∴ $\frac{BE}{PE}=\frac{PB}{FP}$,
∵ ∠B=∠EPF,
∴ △BPE∽△PFE.
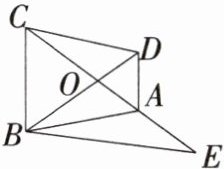
1. 如图,梯形$ABCD$中,$AD // BC$,$AC与BD相交于O$点,过点$B作BE // CD交CA的延长线于点E$。求证:$OC^{2} = OA\cdot OE$。

答案:
证明
∵ CD//BE,
∴ ∠DCO=∠E,又∠DOC=∠BOE,
∴ △OCD∽△OEB,
∴ $\frac{OD}{OB}=\frac{OC}{OE}$,由 AD//BC 同理可得$\frac{OD}{OB}=\frac{OA}{OC}$,
∴ $\frac{OC}{OE}=\frac{OA}{OC}$,即$OC^2=OA·OE$.
∵ CD//BE,
∴ ∠DCO=∠E,又∠DOC=∠BOE,
∴ △OCD∽△OEB,
∴ $\frac{OD}{OB}=\frac{OC}{OE}$,由 AD//BC 同理可得$\frac{OD}{OB}=\frac{OA}{OC}$,
∴ $\frac{OC}{OE}=\frac{OA}{OC}$,即$OC^2=OA·OE$.
2.「2025 四川成都天府七中月考」如图,在菱形$ABCD$中,点$G在边CD$上,连接$AG$并延长,交$BC的延长线于点F$,连接$BD交AF于点E$,连接$CE$。
(1)求证:$EC^{2} = EF\cdot EG$。
(2)若$AB = 6$,$\frac{CE}{EG} = 3$,求$CF$的长。

(1)求证:$EC^{2} = EF\cdot EG$。
(2)若$AB = 6$,$\frac{CE}{EG} = 3$,求$CF$的长。

答案:
解析
(1)证明:
∵ 四边形 ABCD 是菱形,BD 是对角线,
∴ AD=DC,∠ADE=∠CDE,又
∵ DE=DE,
∴ △ADE≌△CDE,
∴ ∠DAE=∠DCE.
∵ AD//BC,
∴ ∠DAE=∠F,
∴ ∠DCE=∠F,
∵ ∠FEC=∠CEG,
∴ △FEC∽△CEG,
∴ $\frac{EC}{EG}=\frac{EF}{EC}$,
∴ $EC^2=EF·EG$.
(2)由
(1)知△FEC∽△CEG,
∴ $\frac{CE}{EG}=\frac{CF}{CG}$,
∵ $\frac{CE}{EG}=3$,
∴ $\frac{CF}{CG}=3$,设 CG=x,则 CF=3x,DG=6-x,
∵ AD//CF,
∴ △ADG∽△FCG,
∴ $\frac{AD}{FC}=\frac{DG}{CG}$,
∴ $\frac{6}{3x}=\frac{6-x}{x}$,解得 x=4 或 x=0(舍去),
∴ CF=3x=12.
(1)证明:
∵ 四边形 ABCD 是菱形,BD 是对角线,
∴ AD=DC,∠ADE=∠CDE,又
∵ DE=DE,
∴ △ADE≌△CDE,
∴ ∠DAE=∠DCE.
∵ AD//BC,
∴ ∠DAE=∠F,
∴ ∠DCE=∠F,
∵ ∠FEC=∠CEG,
∴ △FEC∽△CEG,
∴ $\frac{EC}{EG}=\frac{EF}{EC}$,
∴ $EC^2=EF·EG$.
(2)由
(1)知△FEC∽△CEG,
∴ $\frac{CE}{EG}=\frac{CF}{CG}$,
∵ $\frac{CE}{EG}=3$,
∴ $\frac{CF}{CG}=3$,设 CG=x,则 CF=3x,DG=6-x,
∵ AD//CF,
∴ △ADG∽△FCG,
∴ $\frac{AD}{FC}=\frac{DG}{CG}$,
∴ $\frac{6}{3x}=\frac{6-x}{x}$,解得 x=4 或 x=0(舍去),
∴ CF=3x=12.
查看更多完整答案,请扫码查看


