第65页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
1. 已知点C把线段AB分成两条线段AC、BC,且AC>BC,下列说法错误的是(
A.如果$\frac {AC}{AB}= \frac {BC}{AC}$,那么线段AB被点C黄金分割
B.如果$AC^{2}= AB\cdot BC$,那么线段AB被点C黄金分割
C.如果线段AB被点C黄金分割,那么BC与AB的比叫做黄金比
D.0.618是黄金比的近似值
C
)A.如果$\frac {AC}{AB}= \frac {BC}{AC}$,那么线段AB被点C黄金分割
B.如果$AC^{2}= AB\cdot BC$,那么线段AB被点C黄金分割
C.如果线段AB被点C黄金分割,那么BC与AB的比叫做黄金比
D.0.618是黄金比的近似值
答案:
C 点C把线段AB分成两条线段AC和BC(AC>BC),若$\frac{AC}{AB}=\frac{BC}{AC}$,则称线段AB被点C黄金分割,点C叫做线段AB的黄金分割点,AC与AB的比叫做黄金比.根据黄金分割的定义可知A、B、D中说法正确.如果线段AB被点C黄金分割(AC>BC),那么AC与AB的比叫做黄金比,所以C中说法错误.
2. 跨生物树叶「2025山西长治长子期中」大自然中,一片小小的树叶也蕴含着“黄金分割”的美.黄金分割比的比值为$\frac {\sqrt {5}-1}{2}$,如图,P为线段AB的黄金分割点$(AP>PB)$,如果AB的长度为10cm,那么AP的长度是(

A.$(5\sqrt {5}-5)cm$
B.$(15-5\sqrt {5})cm$
C.6.18cm
D.$(5\sqrt {5}+5)cm$
A
)
A.$(5\sqrt {5}-5)cm$
B.$(15-5\sqrt {5})cm$
C.6.18cm
D.$(5\sqrt {5}+5)cm$
答案:
A
∵P为AB的黄金分割点,AP>PB,
∴$\frac{AP}{AB}=\frac{\sqrt{5}-1}{2}$,
∵AB的长度为10 cm,
∴$\frac{AP}{10}=\frac{\sqrt{5}-1}{2}$,
∴AP=$5(\sqrt{5}-1)=(5\sqrt{5}-5)$cm,故选A.
∵P为AB的黄金分割点,AP>PB,
∴$\frac{AP}{AB}=\frac{\sqrt{5}-1}{2}$,
∵AB的长度为10 cm,
∴$\frac{AP}{10}=\frac{\sqrt{5}-1}{2}$,
∴AP=$5(\sqrt{5}-1)=(5\sqrt{5}-5)$cm,故选A.
3. 学科教材变式特色P98T4「2025山西孝义期中」如图1,在线段AB上找一点C,点C把线段AB分为AC和CB两段,其中AC是较短的一段,若$\frac {AC}{CB}= \frac {CB}{AB}$,则点C叫做线段AB的黄金分割点.如图2所示的是正五角星图案,若点N是线段BE的黄金分割点,且BE= 2,则BN的长为(
A.$\frac {\sqrt {5}-1}{2}$
B.$\frac {\sqrt {5}+1}{2}$
C.$\sqrt {5}-1$
D.$\sqrt {5}+1$
黄金分割 答案D44
C
)A.$\frac {\sqrt {5}-1}{2}$
B.$\frac {\sqrt {5}+1}{2}$
C.$\sqrt {5}-1$
D.$\sqrt {5}+1$
黄金分割 答案D44
答案:
C 【解法一】
∵N是BE的黄金分割点,BN>NE,
∴$\frac{BN}{BE}=\frac{\sqrt{5}-1}{2}$,
∴BN=$2×\frac{\sqrt{5}-1}{2}=\sqrt{5}-1$.故选C.
【解法二】
∵点N是线段BE的黄金分割点,
∴$\frac{EN}{BN}=\frac{BN}{BE}$,
∵BE=2,
∴EN=BE-BN=2-BN,
∴$\frac{2-BN}{BN}=\frac{BN}{2}$,
∴BN=$\sqrt{5}-1$(负值舍去),故选C.
∵N是BE的黄金分割点,BN>NE,
∴$\frac{BN}{BE}=\frac{\sqrt{5}-1}{2}$,
∴BN=$2×\frac{\sqrt{5}-1}{2}=\sqrt{5}-1$.故选C.
【解法二】
∵点N是线段BE的黄金分割点,
∴$\frac{EN}{BN}=\frac{BN}{BE}$,
∵BE=2,
∴EN=BE-BN=2-BN,
∴$\frac{2-BN}{BN}=\frac{BN}{2}$,
∴BN=$\sqrt{5}-1$(负值舍去),故选C.
4. 跨音乐乐器学科教材变式特色P98T1「2023四川达州中考」如图,乐器上的一根弦AB= 80cm,两个端点A,B固定在乐器面板上,支撑点C是靠近点B的黄金分割点,支撑点D是靠近点A的黄金分割点,则支撑点C,D之间的距离为
$(80\sqrt{5}-160)$
cm.(结果保留根号)
答案:
$(80\sqrt{5}-160)$
解析
∵点C是靠近点B的黄金分割点,AB=80 cm,
∴AC=$\frac{\sqrt{5}-1}{2}AB=\frac{\sqrt{5}-1}{2}×80=(40\sqrt{5}-40)$cm,
∵点D是靠近点A的黄金分割点,
∴DB=$\frac{\sqrt{5}-1}{2}AB=\frac{\sqrt{5}-1}{2}×80=(40\sqrt{5}-40)$cm,
∴CD=AC+BD-AB=2$(40\sqrt{5}-40)-80=(80\sqrt{5}-160)$cm,
∴支撑点C,D之间的距离为$(80\sqrt{5}-160)$cm,故答案为$(80\sqrt{5}-160)$.
解析
∵点C是靠近点B的黄金分割点,AB=80 cm,
∴AC=$\frac{\sqrt{5}-1}{2}AB=\frac{\sqrt{5}-1}{2}×80=(40\sqrt{5}-40)$cm,
∵点D是靠近点A的黄金分割点,
∴DB=$\frac{\sqrt{5}-1}{2}AB=\frac{\sqrt{5}-1}{2}×80=(40\sqrt{5}-40)$cm,
∴CD=AC+BD-AB=2$(40\sqrt{5}-40)-80=(80\sqrt{5}-160)$cm,
∴支撑点C,D之间的距离为$(80\sqrt{5}-160)$cm,故答案为$(80\sqrt{5}-160)$.
5. 学科教材变式特色P97随堂练习「2024四川南充中考,★☆」如图,已知线段AB,按以下步骤作图:①过点B作BC⊥AB,使BC= $\frac {1}{2}AB$,连接AC;②以点C为圆心,以BC长为半径画弧,交AC于点D;③以点A为圆心,以AD长为半径画弧,交AB于点E.若AE= mAB,则m的值为(
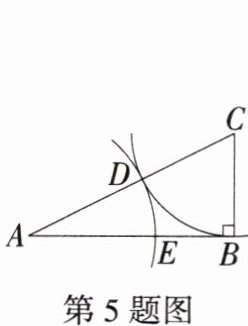
A.$\frac {\sqrt {5}-1}{2}$
B.$\frac {\sqrt {5}-2}{2}$
C.$\sqrt {5}-1$
D.$\sqrt {5}-2$
A
)
A.$\frac {\sqrt {5}-1}{2}$
B.$\frac {\sqrt {5}-2}{2}$
C.$\sqrt {5}-1$
D.$\sqrt {5}-2$
答案:
A 设AB的长为2a,则BC=$\frac{1}{2}AB=a$,在Rt△ABC中,AC=$\sqrt{(2a)^2+a^2}=\sqrt{5}a$.因为CD=CB,AE=AD,所以AE=$(\sqrt{5}-1)a$,则AE=$\frac{\sqrt{5}-1}{2}AB$,所以m的值为$\frac{\sqrt{5}-1}{2}$.故选A.
6. 新考向尺规作图「2025山东济南天桥期中,★☆」如图,在△ABC中,AB= AC,∠BAC= 36°,以点C为圆心,以BC长为半径作弧交AC于点D,再分别以B,D为圆心,以大于$\frac {1}{2}AB$的长为半径作弧,两弧相交于点P,作射线CP交AB于点E,连接DE.下列结论不正确的是(
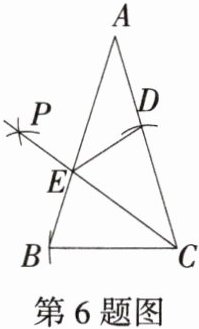
A.∠BCE= 36°
B.BC= AE
C.$\frac {BE}{AC}= \frac {\sqrt {5}-1}{2}$
D.$\frac {S_{△AEC}}{S_{△BEC}}= \frac {\sqrt {5}+1}{2}$
C
)
A.∠BCE= 36°
B.BC= AE
C.$\frac {BE}{AC}= \frac {\sqrt {5}-1}{2}$
D.$\frac {S_{△AEC}}{S_{△BEC}}= \frac {\sqrt {5}+1}{2}$
答案:
C
∵AB=AC,∠BAC=36°,
∴∠ABC=∠ACB=$\frac{180^\circ-\angle BAC}{2}=72^\circ$,由题意得CP平分∠ACB,
∴∠BCE=∠ACE=$\frac{1}{2}\angle ACB=36^\circ$,
∴∠A=∠ACE=36°,
∴AE=CE,
∵∠CEB=∠A+∠ACE=72°,
∴∠ABC=∠CEB,
∴CB=CE,
∴AE=CE=CB,
∵△BCE和△ABC均为顶角为36°的等腰三角形,
∴△BCE∽△BAC,
∴$\frac{BE}{BC}=\frac{BC}{AB}$,
∴$BC^2=BE·AB$,
∴$AE^2=BE·AB$,
∴点E为线段AB的黄金分割点,
∴$\frac{BE}{AE}=\frac{\sqrt{5}-1}{2}$,
∴$\frac{BE}{AC}=\frac{BE}{AB}\neq\frac{\sqrt{5}-1}{2}$,$\frac{S_{\triangle BCE}}{S_{\triangle AEC}}=\frac{BE}{AE}=\frac{\sqrt{5}-1}{2}$,$\frac{S_{\triangle AEC}}{S_{\triangle BCE}}=\frac{2}{\sqrt{5}-1}=\frac{\sqrt{5}+1}{2}$.综上知A、B、D中结论正确,不符合题意,C中结论不正确,符合题意,故选C.
∵AB=AC,∠BAC=36°,
∴∠ABC=∠ACB=$\frac{180^\circ-\angle BAC}{2}=72^\circ$,由题意得CP平分∠ACB,
∴∠BCE=∠ACE=$\frac{1}{2}\angle ACB=36^\circ$,
∴∠A=∠ACE=36°,
∴AE=CE,
∵∠CEB=∠A+∠ACE=72°,
∴∠ABC=∠CEB,
∴CB=CE,
∴AE=CE=CB,
∵△BCE和△ABC均为顶角为36°的等腰三角形,
∴△BCE∽△BAC,
∴$\frac{BE}{BC}=\frac{BC}{AB}$,
∴$BC^2=BE·AB$,
∴$AE^2=BE·AB$,
∴点E为线段AB的黄金分割点,
∴$\frac{BE}{AE}=\frac{\sqrt{5}-1}{2}$,
∴$\frac{BE}{AC}=\frac{BE}{AB}\neq\frac{\sqrt{5}-1}{2}$,$\frac{S_{\triangle BCE}}{S_{\triangle AEC}}=\frac{BE}{AE}=\frac{\sqrt{5}-1}{2}$,$\frac{S_{\triangle AEC}}{S_{\triangle BCE}}=\frac{2}{\sqrt{5}-1}=\frac{\sqrt{5}+1}{2}$.综上知A、B、D中结论正确,不符合题意,C中结论不正确,符合题意,故选C.
查看更多完整答案,请扫码查看


