《2025年5年中考3年模拟九年级数学上册北师大版》

8. [2025安徽合肥经开区月考,★☆] 如图,四边形$ABCD$是平行四边形,$G是DC$的延长线上一点,$AG分别与DB$,$CB交于点E$,$F$,下列结论错误的是(D)

A.$\triangle ADG \backsim \triangle FCG$
B.$\triangle ADE \backsim \triangle FBE$
C.$\triangle ABE \backsim \triangle GDE$
D.$\triangle ABF \backsim \triangle GDE$

答案： D
∵四边形ABCD是平行四边形，
∴AD//BC,
∴△ADG∽△FCG,△ADE∽△FBE,故选项A、B均正确，不符合题意;
∵四边形ABCD是平行四边形，
∴AB//DC,
∴△ABE∽△GDE,故选项C正确,不符合题意;无法证明△ABF∽△GDE,故选项D错误,符合题意.故选D.

9. 学科特色 一线三等角模型 [2025湖南娄底娄星期中,★☆] 如图,$\triangle ABC$为等边三角形,点$D$,$E分别在边BC$,$AB$上,$\angle ADE = 60^{\circ}$。若$BD = 4DC$,$DE = 2.4$,则$AD$的长为(C)

A.1.8
B.2.4
C.3
D.3.2

答案： C
∵△ABC是等边三角形，
∴BC=AC,∠B=∠C=60°,
∴∠CAD+∠ADC=120°,
∵∠ADE=60°,
∴∠BDE+∠ADC=120°,
∴∠CAD=∠BDE,
∴△ADC ∽△DEB,
∴$\frac{AD}{DE}=\frac{AC}{DB}$,
∵BD=4DC,
∴设DC=x,则BD=4x,
∴BC=AC=5x,
∴$\frac{AD}{2.4}=\frac{5x}{4x}$,
∴AD=3,故选C.

10. [2024河北石家庄二十八中月考,★☆] 如图,$\triangle ABC$中,$CE \perp AB$,垂足为$E$,$BD \perp AC$,垂足为$D$,$CE与BD交于点F$,则图中相似三角形有(A)

A.6对
B.5对
C.4对
D.3对

答案： A
∵BD⊥AC,CE⊥AB,
∴∠AEC=∠ADB=90°,∠BEF=∠CDF=90°,
又
∵∠A=∠A,∠EFB=∠DFC,
∴△AEC∽△ADB,△BEF∽△CDF,
∵∠EBF=∠ABD,∠BEF=∠ADB=90°,
∴△BEF∽△BDA∽△CEA∽△CDF,
∴共有6对相似三角形.故选A.

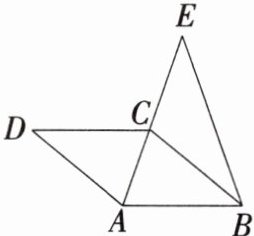
11. [2025山东聊城月考,★☆] 如图,四边形$ABCD$为菱形,点$E在AC$的延长线上,$\angle ACD = \angle ABE$。
(1) 求证：$\triangle ABC \backsim \triangle AEB$。
(2) 当$AB = 6$,$AC = 4$时,求$CE$的长。

答案： 解析　
(1)证明:
∵四边形ABCD为菱形,
∴∠ACD=∠BCA,
∵∠ACD=∠ABE,
∴∠BCA=∠ABE,
∵∠BAC=∠EAB,
∴△ABC∽△AEB.
(2)
∵△ABC∽△AEB,
∴$\frac{AB}{AE}=\frac{AC}{AB}$,
∵AB=6,AC=4,
∴$\frac{6}{AE}=\frac{4}{6}$,
∴AE=$\frac{36}{4}=9$,
∴CE=AE−AC=9−4=5.

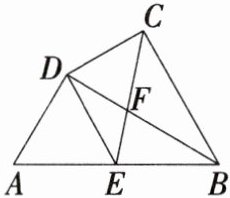
12. [2024湖南益阳期中,★☆] 如图,四边形$ABCD$中,$BD平分\angle ABC$,$\angle ADB = \angle DCB = 90^{\circ}$,$E为AB$的中点,$CE与BD交于点F$。
(1) 求证：$\triangle ABD \backsim \triangle DBC$。
(2) 求证：$DE // BC$。
(3) 若$DF : BF = 2 : 3$,$CD = 6$,求$DE$的长。

答案： 解析　
(1)证明:
∵BD平分∠ABC,
∴∠CBD=∠ABD,
∵∠ADB=∠DCB,
∴△ABD∽△DBC.
(2)证明:
∵E是AB的中点,∠ADB=90°,
∴DE=BE=AE,
∴∠EDB=∠EBD,
∵∠CBD=∠EBD,
∴∠CBD=∠EDB,
∴DE//BC.
(3)
∵∠EDF=∠CBF,∠EFD=∠CFB,
∴△DEF∽△BCF,
∴$\frac{DF}{BF}=\frac{DE}{BC}$,
∵DF∶BF=2∶3,
∴$\frac{DE}{BC}=\frac{2}{3}$,
∴$\frac{\frac{1}{2}AB}{BC}=\frac{2}{3}$,
∴$\frac{AB}{BC}=\frac{4}{3}$.
设AB=4m,则BC=3m,由
(1)知△ABD∽△DBC,
∴$\frac{AB}{BD}=\frac{BD}{BC}=\frac{AD}{CD}$,
∵CD=6,
∴$\frac{4m}{BD}=\frac{BD}{3m}=\frac{AD}{6}$,
∴BD=$2\sqrt{3}m$,AD=$4\sqrt{3}$,
∵$AD^2+BD^2=AB^2$,
∴$(4\sqrt{3})^2+(2\sqrt{3}m)^2=(4m)^2$,解得m=$2\sqrt{3}$(舍去负值),
∴AB=4m=$8\sqrt{3}$,
∴DE=$\frac{1}{2}AB=4\sqrt{3}$.

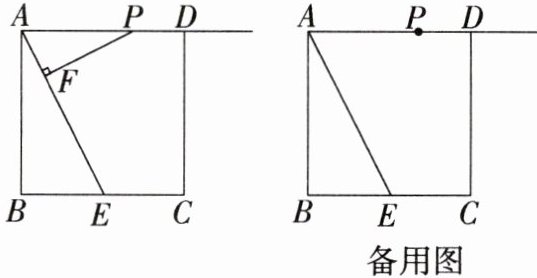
13. 新课标 推理能力 如图,正方形$ABCD$的边长为4,$E是BC$边的中点,点$P在射线AD$上,过$P作PF \perp AE于F$。
(1) 求证：$\triangle PFA \backsim \triangle ABE$。
(2) 当点$P在射线AD$上运动时,设$PA = x$,是否存在实数$x$,使以$P$,$F$,$E为顶点的三角形与\triangle ABE$相似？若存在,请求出$x$的值；若不存在,请说明理由。

答案：
解析
∵四边形ABCD是正方形，
∴AD//BC,∠B=90°.
(1)证明:
∵AD//BC,
∴∠PAF=∠AEB.
∵∠PFA=∠B=90°,
∴△PFA∽△ABE.
(2)存在
∵PF⊥AE,
∴∠PFE=90°=∠B.
∴当以P,F,E为顶点的三角形与△ABE相似时,有两种情况:如图①,若△EFP∽△ABE,则∠PEF=∠EAB,
∴PE//AB.
∴四边形ABEP为矩形.
∴PA=EB=2,即x=2.
　　　　　
如图②,若△PFE∽△ABE,则∠PEF=∠AEB.
∵∠PAF=∠AEB,
∴∠PEF=∠PAF.
∴PE=PA.
∵PF⊥AE,
∴点F为AE的中点
∵AE=$\sqrt{AB^2+BE^2}=2\sqrt{5}$,
∴EF=$\frac{1}{2}AE=\sqrt{5}$
∵$\frac{PE}{AE}=\frac{EF}{EB}$,即$\frac{PE}{2\sqrt{5}}=\frac{\sqrt{5}}{2}$,
∴PE=5,即x=5.
综上可知,x的值为2或5.