《2025年5年中考3年模拟九年级数学上册北师大版》

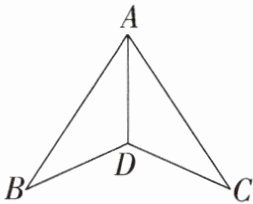
7. [2022 广西玉林中考] 问题情境:在数学探究活动中,老师给出了如图所示的图形及下面三个等式:① $A B= A C$;② $D B= D C$;③ $\angle B A D= \angle C A D$. 若以其中两个等式作为已知条件,能否得到余下一个等式成立?
解决方案:探究 $\triangle A B D$ 与 $\triangle A C D$ 全等.
问题解决:
(1) 当选择①②作为已知条件时, $\triangle A B D$ 与 $\triangle A C D$ 全等吗? ____(填“全等”或“不全等”),理由是____.
(2) 当任意选择两个等式作为已知条件时,请用画树状图法或列表法求 $\triangle A B D \cong \triangle A C D$ 的概率.

答案：
7.解析　
(1)全等；三边分别相等的两个三角形全等.
(2)画树状图如下:

共有六种等可能的情况，符合条件的有①②，①③，②①，③①四种，则P($\triangle ABD\cong \triangle ACD$)$=\frac{4}{6}=\frac{2}{3}$.

8. [2024 四川资阳中考] 我国古诗词源远流长. 某校组织学生开展了以“赏诗词之美、寻文化之根、铸民族之魂”为主题的古诗词知识竞赛活动. 为了解学生对古诗词的掌握情况,该校随机抽取了部分学生的竞赛成绩,将成绩分为 A,B,C,D 四个等级,并绘制成如图所示的两幅不完整的统计图:

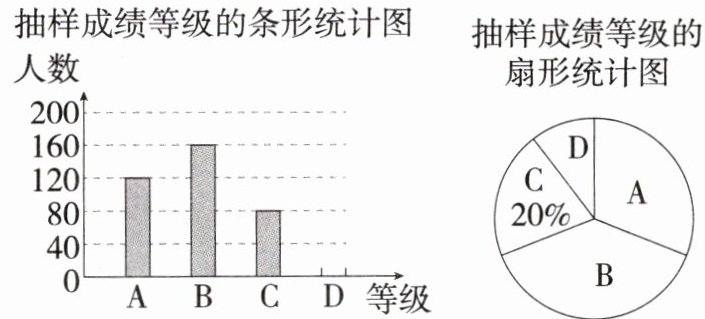
(1) 本次共抽取了____名学生的竞赛成绩,并补全条形统计图.
(2) 若该校共有 2000 人参加本次竞赛活动,估计竞赛成绩为 B 等级的学生人数.
(3) 学校在竞赛成绩为 A 等级的甲、乙、丙、丁这 4 名学生中,随机选取 2 人参加经典诵读活动,用画树状图或列表的方法求出甲、乙两人中恰好有 1 人被选中的概率.

答案：
8.解析　
(1)$80÷ 20\% =400$(人)，本次共抽取了400名学生的竞赛成绩，
∴成绩为D等级的学生人数为$400 - 120 - 160 - 80 = 40$，补全条形统计图如下:

(2)$2000× \frac{160}{400}=800$(人).答:估计竞赛成绩为B等级的学生人数为800.
(3)画树状图如下:

共有12种等可能的结果，其中甲、乙两人中恰好有1人被选中的结果有8种，
∴甲、乙两人中恰好有1人被选中的概率为$\frac{8}{12}=\frac{2}{3}$.

9. 小亮和爸爸搭乘高铁外出游玩. 在网上购票时,系统已将两人分配到同一车厢同一排(下图是高铁座位示意图). 用列表法求小亮和爸爸分配的座位挨在一起(过道两侧也可认为是座位挨在一起)的概率.

答案： 9.解析　列表如下:
A
B
C
D
F
A
A,B
A,C
A,D
A,F
B
B,A
B,C
B,D
B,F
C
C,A
C,B
C,D
C,F
D
D,A
D,B
D,C
D,F
F
F,A
F,B
F,C
F,D
共有20种等可能的结果，其中小亮和爸爸的座位挨在一起的结果有8种，故小亮和爸爸分配的座位挨在一起的概率是$\frac{8}{20}=\frac{2}{5}$.