《2025年5年中考3年模拟九年级数学上册北师大版》

6. 跨化学化学变化 [2024甘肃临夏州中考,☆☆]物理变化和化学变化的区别在于是否有新物质的生成.某学习小组在延时课上制作了A,B,C,D四张卡片,四张卡片除图片内容不同外,其他没有区别,放置于暗箱中摇匀.

A.铁钉生锈 B.滴水成冰 C.矿石粉碎 D.牛奶变质
(1)小临从四张卡片中随机抽取一张,抽中C卡片的概率是______.
(2)小夏从四张卡片中随机抽取两张,用列表法或画树状图法求小夏抽取两张卡片内容均为化学变化的概率.

答案：

(1)$\frac{1}{4}$
(2)四张卡片内容中是的为A和D，画树状图如下: 共有12种等可能的结果，其中小夏抽取两张卡片内容均为化学变化的结果AD，DA，共2种，
∴小夏抽取两张卡片内容均为化学变化率为$\frac{2}{12}=\frac{1}{6}$

1. [2024北京中考]不透明袋子中仅有红、黄小球各一个,两个小球除颜色外无其他差别.从中随机摸出一个小球,放回并摇匀,再从中随机摸出一个小球,则两次摸出的都是红球的概率是 (A)
A.$\frac{1}{4}$
B.$\frac{1}{3}$
C.$\frac{1}{2}$
D.$\frac{3}{4}$

答案： 【解析】：
这个问题是一个典型的概率问题，可以通过树状图或表格来求解。
首先，我们分析第一次摸球的情况。由于袋子里有红球和黄球各一个，所以摸出红球的概率是$\frac{1}{2}$。
然后，我们分析第二次摸球的情况。由于第一次摸出的球被放回了袋子，并摇匀，所以第二次摸球的概率与第一次相同，即摸出红球的概率也是$\frac{1}{2}$。
接下来，我们利用树状图或表格来列举所有可能的情况，并找出两次都摸出红球的情况。
所有可能的情况有：红-红，红-黄，黄-红，黄-黄，共4种情况。
其中两次都摸出红球的情况只有1种，即红-红。
所以，两次摸出的都是红球的概率是$\frac{1}{4}$。
【答案】：
A. $\frac{1}{4}$。

7. 新课标应用意识 某迷宫游戏地图如图1所示,嘉淇从点O出发,只要遇到一扇门就必须从里圈走到外圈,然后随机向左转或向右转后继续行进(如走出A门后,若左拐行进会从E门走出;若右拐行进会从D门走出),且这两种情况可能性相同,规定:走进死胡同就算失败.

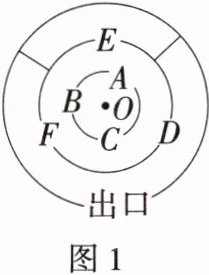
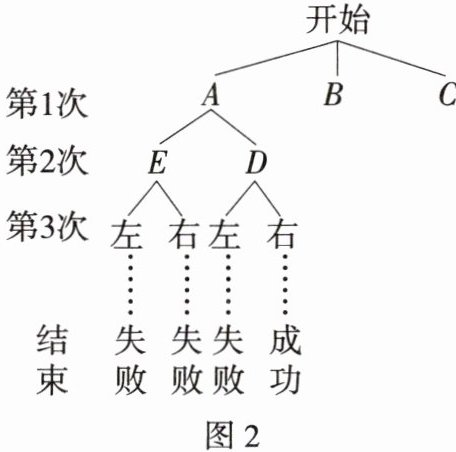
(1)若嘉淇从“A”“B”“C”门走出的可能性均相同,则选择“A”门的概率为______.
(2)补全图2的树状图,并计算嘉淇成功走出该迷宫的概率.

答案：

(1)$\frac{1}{3}$；
(2)补全树状图如图所示. 由树状图可知，共有12种等可能的结果，其中成功走出迷宫的结果有4种，
∴嘉淇成功走出迷宫的概率为$\frac{4}{12}=\frac{1}{3}$

2. 在桌面上放有四张背面朝上且完全一样的卡片,卡片正面分别标有数字1,2,3,4,小明、小红、小亮三人依次从中抽取一张卡片(不放回),小明抽取的卡片上的数字作百位,小红抽取的卡片上的数字作十位,小亮抽取的卡片上的数字作个位,则抽取的卡片上的数字组成的三位数为偶数的概率是$\frac{1}{2}$.

答案： $\frac{1}{2}$