《2025年5年中考3年模拟九年级数学上册北师大版》

1.「2025天津一中月考」下列方程是一元二次方程的是(B)
A.$ax^{2}+bx+c= 0$
B.$x^{2}= 0$
C.$x^{2}+\frac {1}{x}= 1$
D.$(x-1)^{2}+1= x^{2}$

答案： 选项A,当a=0时,方程为bx+c=0,不是一元二次方程,该选项不合题意;选项B,方程$x^{2}=0$是一元二次方程,该选项符合题意;选项C,方程$x^{2}+\frac {1}{x}=1$的左边不是整式,不是一元二次方程,该选项不合题意;选项D,方程$(x-1)^{2}+1=x^{2}$整理为$-2x+2=0$,不是一元二次方程,该选项不合题意.故选B.

2.根据下列表格的对应值,判断方程$ax^{2}+bx+c= 0(a≠0,a,b,c$为常数)一个解的范围是(C)
A.$3.22＜x＜3.23$
B.$3.23＜x＜3.24$
C.$3.24＜x＜3.25$
D.$3.25＜x＜3.26$

答案： 当x=3.24时,y=-0.02,当x=3.25时,y=0.03,
∴方程$ax^{2}+bx+c=0$的一个解的范围是3.24＜x＜3.25,故选C.

3.「2025甘肃张掖期末」珍珍将方程$x^{2}-4x-2= 0化为(x+p)^{2}= q$的形式时,得到ρ的值为2,q的值为6,则珍珍所得结果(B)
A.正确
B.不正确,p的值应为-2
C.不正确,q的值应为2
D.不正确,q的值应为4

答案： $x^{2}-4x=2$,$x^{2}-4x+4=2+4$,$(x-2)^{2}=6$,
∴p=-2,q=6,故选B.

4.「2024黑龙江牡丹江中考」一种药品原价每盒48元,经过两次降价后每盒27元,两次降价的百分率相同,则每次降价的百分率为(C)
A.20%
B.22%
C.25%
D.28%

答案： 设每次降价的百分率为x,由题意,得$48(1-x)^{2}=27$,解得$x_{1}=\frac {1}{4}=25\%$,$x_{2}=\frac {7}{4}$(舍去).故选C.

5.「2024河北中考」淇淇在计算正数α的平方时,误算成α与2的积,求得的答案比正确答案小1,则$a=$(C)
A.1
B.$\sqrt {2}-1$
C.$\sqrt {2}+1$
D.1或$\sqrt {2}+1$

答案： 根据题意得,$a^{2}-2a=1$,解得$a=1\pm \sqrt {2}$,
∵a是正数,
∴$a=\sqrt {2}+1$.故选C.

6.「2025河北保定阜平期中」小明参加了一次“朋友圈点名"活动,他将问题和自己的答案在朋友圈
主检测
二次方程
中发布,同时还按规定“@”一定数量的其他人(未参与过该活动)参与活动,如果收到小明邀请的人也同样参与了该活动并按规定“@”一定数量的其他人(未参与过该活动),且从小明开始算起,转发两轮后共有91人被邀请参与该活动.设参与该活动后规定“@”x人,则可列方程为(B)
A.$x^{2}= 91$
B.$1+x+x^{2}= 91$
C.$1+x+x(1+x)= 91$
D.$1+x^{2}= 91$

答案：
∵参与该活动后规定“@”x人,
∴第一轮中新增x人被邀请参与该活动,第二轮中新增$x^{2}$人被邀请参与该活动.根据题意得$1+x+x^{2}=91$.故选B.

7.已知等腰$△ABC$的底边长为3,两腰长恰好是关于x的一元二次方程$\frac {1}{2}kx^{2}-(k+3)x+6= 0$的两根,则$△ABC$的周长为(B)
A.6.5
B.7
C.6.5或7
D.8

答案：
∵等腰△ABC的两腰长恰好是关于x的一元二次方程$\frac {1}{2}kx^{2}-(k+3)x+6=0$的两根,
∴$\Delta =[-(k+3)]^{2}-4×\frac {1}{2}k×6=0$,解得$k_{1}=k_{2}=3$,
∴一元二次方程为$\frac {3}{2}x^{2}-6x+6=0$,
∴两腰长之和为$\frac {-6}{\frac {3}{2}}=4$,
∴△ABC的周长为4+3=7.故选B.

8.「2024河南省实验中学月考」$m=$1时,关于x的方程$(m+1)x^{m^{2}+1}+mx+5= 0$是一元二次方程.

答案： 答案 1 解析
∵关于x的方程$(m+1)x^{m^{2}+1}+mx+5=0$是一元二次方程,
∴$m^{2}+1=2$且$m+1≠0$,解得m=1.

9.「2024四川巴中中考」已知方程$x^{2}-2x+k= 0$的一个根为-2,则方程的另一个根为4.

答案： 答案 4 解析 设方程的另一个根为m,因为方程的一个根为-2,所以-2+m=2,解得m=4,所以方程的另一个根为4.故答案为4.

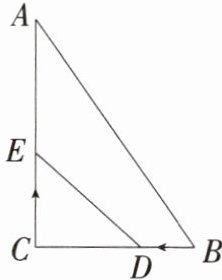
10.「2025辽宁鞍山期中」如图所示,$△ABC$中,$∠C= 90^{\circ },AC= 8cm,BC= 6cm$,点D从B点开始沿BC向C点以1 cm/s的速度移动,点E从C点开始沿CA向A点以2 cm/s的速度移动,如果D、E分别从B、C同时出发,那么2或4秒后,线段DE将$△ABC$分成面积为1:2的两部分.

答案： 答案 2或4 解析 设t秒后,线段DE将△ABC分成面积为1:2的两部分,根据题意,知CD=BC-BD=(6-t)cm,CE=2t cm.
∵线段DE将△ABC分成面积为1:2的两部分,
∴$S_{\triangle CDE}=\frac {1}{3}S_{\triangle ABC}$或$S_{\triangle CDE}=\frac {2}{3}S_{\triangle ABC}$,根据三角形的面积公式,得$\frac {1}{2}(6-t)\cdot 2t=\frac {1}{3}×\frac {1}{2}×6×8$或$\frac {1}{2}(6-t)\cdot 2t=\frac {2}{3}×\frac {1}{2}×6×8$,整理得$t^{2}-6t+8=0$①或$t^{2}-6t+16=0$②,解①得$t_{1}=2$,$t_{2}=4$,解②得该方程无实数根.故2秒或4秒后,线段DE将△ABC分成面积为1:2的两部分.故答案为2或4.