第4页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
9. 「2025江苏南京五十中月考,」如图,在四边形$ABCD$中,$E$、$F$、$G$、$H分别是线段AD$、$BD$、$BC$、$AC$的中点,要使四边形$EFGH$是菱形,需添加的条件是(
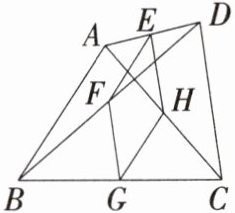
A.$AC= BD$
B.$AC\perp BD$
C.$AB= CD$
D.$AB\perp CD$
C
)
A.$AC= BD$
B.$AC\perp BD$
C.$AB= CD$
D.$AB\perp CD$
答案:
C
10. 「2023上海奉贤模拟,」用尺规在一个平行四边形内作菱形$ABCD$,下列作法中错误的是(
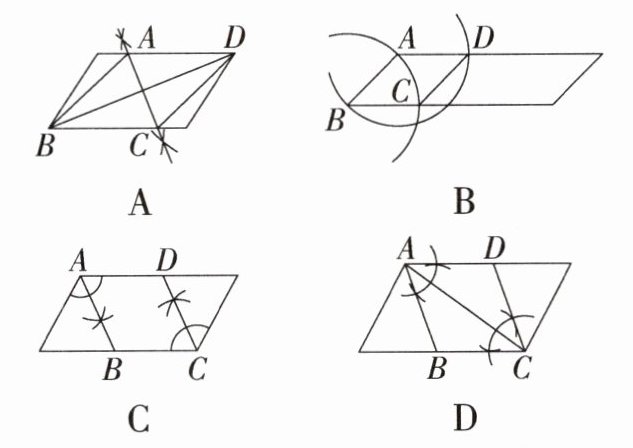
C
)
答案:
C
11.「2025辽宁沈阳大东月考,」如图,已知点$A$,$D$,$C$,$B$在同一条直线上,且$AD= BC$,$AE= BF$,$CE= DF$。
(1)求证:$AE// BF$。
(2)若$DF= FC$,求证:四边形$DECF$是菱形。

(1)求证:$AE// BF$。
(2)若$DF= FC$,求证:四边形$DECF$是菱形。

答案:
(1)
∵AD = BC,
∴AD + CD = BC + CD,
∴AC = BD,
∵AE = BF,CE = DF,
∴△AEC≌△BFD(SSS),
∴∠A = ∠B,
∴AE//BF.
(2)
∵△AEC≌△BFD,
∴∠ECA = ∠FDB,
∴EC//DF,
∵EC = DF,
∴四边形DECF是平行四边形,
∵DF = FC,
∴四边形DECF是菱形.
(1)
∵AD = BC,
∴AD + CD = BC + CD,
∴AC = BD,
∵AE = BF,CE = DF,
∴△AEC≌△BFD(SSS),
∴∠A = ∠B,
∴AE//BF.
(2)
∵△AEC≌△BFD,
∴∠ECA = ∠FDB,
∴EC//DF,
∵EC = DF,
∴四边形DECF是平行四边形,
∵DF = FC,
∴四边形DECF是菱形.
12. 「2024江苏扬州中考,」如图1,将两个宽度相等的矩形纸条叠放在一起,得到四边形$ABCD$。
(1)试判断四边形$ABCD$的形状,并说明理由。
(2)已知矩形纸条宽度为2cm,将矩形纸条旋转至如图2所示的位置时,四边形$ABCD的面积为8cm^{2}$,求此时直线$AD$、$CD所夹锐角\angle 1$的度数。

(1)试判断四边形$ABCD$的形状,并说明理由。
(2)已知矩形纸条宽度为2cm,将矩形纸条旋转至如图2所示的位置时,四边形$ABCD的面积为8cm^{2}$,求此时直线$AD$、$CD所夹锐角\angle 1$的度数。

答案:
(1)四边形ABCD是菱形,理由如下:如图1,作CH⊥AB,垂足为H,CG⊥AD,垂足为G,
∵两个纸条为矩形,
∴AB//CD,AD//BC,
∴四边形ABCD是平行四边形,
∵S▱ABCD = AB·CH = AD·CG,且CH = CG,
∴AB = AD,
∴四边形ABCD是菱形.
(2)如图2,作AM⊥CD,垂足为M,
∵S菱形ABCD = CD·AM = 8 cm²,且AM = 2 cm,
∴CD = 4 cm,
∴AD = CD = 4 cm.在Rt△ADM中,AM = $\frac{1}{2}$AD,
∴∠1 = 30°.
(1)四边形ABCD是菱形,理由如下:如图1,作CH⊥AB,垂足为H,CG⊥AD,垂足为G,
∵两个纸条为矩形,
∴AB//CD,AD//BC,
∴四边形ABCD是平行四边形,
∵S▱ABCD = AB·CH = AD·CG,且CH = CG,
∴AB = AD,
∴四边形ABCD是菱形.
(2)如图2,作AM⊥CD,垂足为M,
∵S菱形ABCD = CD·AM = 8 cm²,且AM = 2 cm,
∴CD = 4 cm,
∴AD = CD = 4 cm.在Rt△ADM中,AM = $\frac{1}{2}$AD,
∴∠1 = 30°.
13. 如图,在平行四边形$ABCD$中,$AB\perp AC$,$AB= 6$,$BC= 10$,点$P从点B$出发,沿射线$BC$方向运动,同时点$Q从点D$出发,沿$DA$方向运动,当点$Q运动到点A$时,点$Q$停止运动,设运动的时间为$t\mathrm{s}$。
(1)若点$P$每秒运动3个单位,点$Q$每秒运动1个单位,求当$t$为何值时,以$P$、$C$、$D$、$Q$为顶点的四边形为平行四边形。
(2)当点$P每秒运动m$个单位,点$Q每秒运动n$个单位时,若运动中能使以点$P$、$C$、$D$、$Q$为顶点的四边形为菱形,请直接写出$m$、$n$的数量关系。

(1)若点$P$每秒运动3个单位,点$Q$每秒运动1个单位,求当$t$为何值时,以$P$、$C$、$D$、$Q$为顶点的四边形为平行四边形。
(2)当点$P每秒运动m$个单位,点$Q每秒运动n$个单位时,若运动中能使以点$P$、$C$、$D$、$Q$为顶点的四边形为菱形,请直接写出$m$、$n$的数量关系。

答案:
(1)①如图,当点P在线段BC上时,DQ = t,PC = 10 - 3t,
∵四边形ABCD是平行四边形,
∴AD//BC.若以点P、C、D、Q为顶点的四边形是平行四边形,则DQ = PC,
∴t = 10 - 3t,
∴t = 2.5.②当点P在BC的延长线上时,PC = 3t - 10.若以点P、C、D、Q为顶点的四边形是平行四边形,则DQ = PC,
∴t = 3t - 10,
∴t = 5.综上,当t的值为2.5或5时,以点P、C、D、Q为顶点的四边形为平行四边形.
(2)①当点P在线段BC上时,若以点P、C、D、Q为顶点的四边形是菱形,则DQ = PC = CD = 6,
∴nt = 10 - mt = 6,
∴mt = 4,
∴$\frac{m}{n}$ = $\frac{2}{3}$,
∴3m = 2n.②如图,当点P在BC的延长线上时,连接PQ,交CD于点E,
∵AB⊥AC,
∴∠BAC = 90°,
∴AC = $\sqrt{BC^{2}-AB^{2}}$ = $\sqrt{10^{2}-6^{2}}$ = 8.
∵四边形ABCD是平行四边形,
∴CD//AB,
∴∠ACD = ∠BAC = 90°.若以点P、C、D、Q为顶点的四边形是菱形,则PQ⊥CD,CE = DE = 3,PE = QE,DQ = PC,
∴PQ//AC.
∵AD//BC,
∴四边形ACPQ是平行四边形,
∴PQ = AC = 8,
∴QE = PE = 4,
∴DQ = PD = $\sqrt{QE^{2}+DE^{2}}$ = $\sqrt{4^{2}+3^{2}}$ = 5,
∴nt = mt - 10 = 5,
∴mt = 15,
∴m = 3n.综上,当3m = 2n或m = 3n时,以点P、C、D、Q为顶点的四边形为菱形.
(1)①如图,当点P在线段BC上时,DQ = t,PC = 10 - 3t,
∵四边形ABCD是平行四边形,
∴AD//BC.若以点P、C、D、Q为顶点的四边形是平行四边形,则DQ = PC,
∴t = 10 - 3t,
∴t = 2.5.②当点P在BC的延长线上时,PC = 3t - 10.若以点P、C、D、Q为顶点的四边形是平行四边形,则DQ = PC,
∴t = 3t - 10,
∴t = 5.综上,当t的值为2.5或5时,以点P、C、D、Q为顶点的四边形为平行四边形.
(2)①当点P在线段BC上时,若以点P、C、D、Q为顶点的四边形是菱形,则DQ = PC = CD = 6,
∴nt = 10 - mt = 6,
∴mt = 4,
∴$\frac{m}{n}$ = $\frac{2}{3}$,
∴3m = 2n.②如图,当点P在BC的延长线上时,连接PQ,交CD于点E,
∵AB⊥AC,
∴∠BAC = 90°,
∴AC = $\sqrt{BC^{2}-AB^{2}}$ = $\sqrt{10^{2}-6^{2}}$ = 8.
∵四边形ABCD是平行四边形,
∴CD//AB,
∴∠ACD = ∠BAC = 90°.若以点P、C、D、Q为顶点的四边形是菱形,则PQ⊥CD,CE = DE = 3,PE = QE,DQ = PC,
∴PQ//AC.
∵AD//BC,
∴四边形ACPQ是平行四边形,
∴PQ = AC = 8,
∴QE = PE = 4,
∴DQ = PD = $\sqrt{QE^{2}+DE^{2}}$ = $\sqrt{4^{2}+3^{2}}$ = 5,
∴nt = mt - 10 = 5,
∴mt = 15,
∴m = 3n.综上,当3m = 2n或m = 3n时,以点P、C、D、Q为顶点的四边形为菱形.
查看更多完整答案,请扫码查看


