《2025年5年中考3年模拟九年级数学上册北师大版》

1.「2023黑龙江哈尔滨中考」为了改善居民生活环境,某小区对一块矩形空地进行绿化,这块空地的长比宽多6米,面积为720平方米,设矩形空地的长为x米,根据题意,所列方程正确的是(A)
A.$ x(x - 6) = 720 $
B.$ x(x + 6) = 720 $
C.$ x(x - 6) = 360 $
D.$ x(x + 6) = 360 $

答案： A 矩形空地的长为x米,则矩形空地的宽为(x - 6)米，由题意可得x(x - 6)=720,故选A.

2.「2025山东商河期中」如图,在长为100m,宽为50m的矩形空地上修筑四条宽度相等的小路,若余下的部分全部种上花卉,且花圃的面积是$3600m^2,$则小路的宽是(A)

A.5m
B.70m
C.5m或70m
D.10m

答案： A 设小路的宽是x m,则余下的部分可合成长为(100 - 2x)m,宽为(50 - 2x)m的矩形,根据题意得(100 - 2x)(50 - 2x)=3600,整理得$x^{2}-75x+350=0$,解得$x_{1}=5$,$x_{2}=70$(不符合题意,舍去),
∴小路的宽是5 m.故选A.

3.「2025河北任丘期中」某校从本学期开始实施劳动教育,在学校靠墙(墙长22米)的一块空地上,开辟出一块矩形菜地,如图所示,矩形菜地的另外三边用一根长49米的绳子围成,并留1米宽的门,若想开辟成面积为300平方米的菜地,则菜地垂直于墙的一边的长为(C)
A.10米
B.12米
C.15米
D.不存在

答案： C 设菜地垂直于墙的一边的长为x米,由题意列方程可得x(49 + 1 - 2x)=300,解得$x_{1}=10$,$x_{2}=15$.当x = 10时,49 + 1 - 2x = 30,30＞22,不符合题意,舍去;当x = 15时,49 + 1 - 2x = 20,20＜22,符合题意.所以菜地垂直于墙的一边的长为15米.故选C.

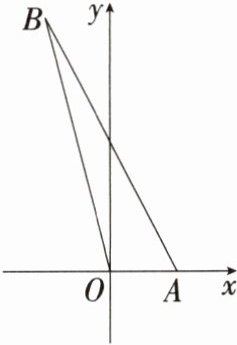
4. 教材变式 如图,由点 $ A(a, 0) $,$ O(0, 0) $,$ B(-a, a + 3)(a ＞ 0) $ 确定的三角形的面积为2,求a的值.

方程在实际生活中的应用 答案D22

答案： 解析 由△AOB的面积为2,得$\frac{1}{2}a(a + 3)=2$.化简,得$a^{2}+3a - 4=0$,解得a = - 4(不符合题意,舍去)或a = 1.故a的值为1.

5.「2025河北衡水九中期中,」在一块长16m,宽12m的矩形荒地上,要建造一个花园,要求花园面积是荒地面积的一半,下面分别是小华与小芳的设计方案.

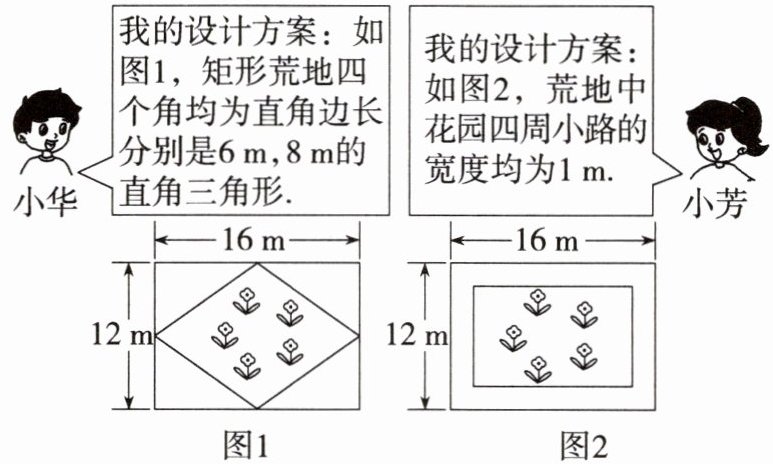
(1)同学们都认为小华的方案是正确的,但对小芳的方案是否符合条件有不同意见,你认为小芳的方案符合条件吗？若不符合,请用方程的方法说明理由.
(2)你还有其他的设计方案吗？请在图3中画出你所设计的草图,将花园部分涂上颜色,并写出你的设计方案.

答案：

(1)不符合.理由:设小路的宽度均为x m,根据题意得$(16 - 2x)(12 - 2x)=\frac{1}{2}×12×16$,解得$x_{1}=2$,$x_{2}=12$.但$x_{2}=12$不符合题意，应舍去，
∴x = 2.
∴小芳的方案不符合条件.
(2)答案不唯一. 例如: 左边的图形，取上边的边的中点作为三角形的顶点，下边的边两个端点为三角形的另外两个顶点，此三角形的面积等于矩形面积的一半;右边的图形有横竖两条小路，且小路在每一处的宽都相同，小路的宽为4米时，除去小路后剩下部分的面积为矩形面积的一半.