第20页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
8.如图,三位同学分别站在一个直角三角形的三个顶点处做投圈游戏,目标物放在斜边AC的中点O处,已知$AC= 6m$,则点B到目标物的距离是
3
m.
答案:
答案 3
解析
∵∠ABC = 90°,O是斜边AC的中点,
∴BO = $\frac{1}{2}$AC = 3m。
解析
∵∠ABC = 90°,O是斜边AC的中点,
∴BO = $\frac{1}{2}$AC = 3m。
9.「2025河南平顶山期中」小明用四根长度相等的木条制作了能够活动的菱形学具,他先将学具活动成如图(1)所示的菱形,并测得$∠ABC= 60^{\circ }$,接着将学具活动成如图(2)所示的正方形,并测得对角线$AC= 20\sqrt {2}$,则图(1)中菱形的对角线BD的长为____
20√3
.
答案:
答案 20√3
解析 在正方形ABCD中,∠ABC = 90°,
∴AB² + CB² = AC²,
∵AB = CB,AC = 20√2,
∴AB = BC = 20。在题图
(1)中,连接AC交BD于点O(图略),在菱形ABCD中,AC⊥BD,AB = BC = 20,
∵∠ABC = 60°,
∴△ABC为等边三角形,
∴∠ABO = 30°,
∴OA = $\frac{1}{2}$AB = 10,
∴OB = $\sqrt{AB² - AO²}$ = 10√3,
∴BD = 2OB = 20√3,故答案为20√3。
解析 在正方形ABCD中,∠ABC = 90°,
∴AB² + CB² = AC²,
∵AB = CB,AC = 20√2,
∴AB = BC = 20。在题图
(1)中,连接AC交BD于点O(图略),在菱形ABCD中,AC⊥BD,AB = BC = 20,
∵∠ABC = 60°,
∴△ABC为等边三角形,
∴∠ABO = 30°,
∴OA = $\frac{1}{2}$AB = 10,
∴OB = $\sqrt{AB² - AO²}$ = 10√3,
∴BD = 2OB = 20√3,故答案为20√3。
10.「2023河南省实验中学月考」如图,在边长为$2\sqrt {2}$的正方形ABCD中,点E,F分别是边AB,BC的中点,连接EC,FD,点G,H分别是EC,FD的中点,连接GH,则GH的长度为____.
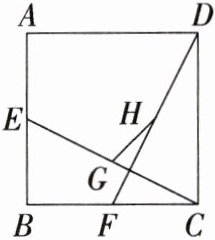

答案:
答案 1
解析 【解法一】连接CH并延长交AD于P,连接PE,如图1,
∵四边形ABCD是正方形,且边长为2√2,
∴∠A = 90°,AD//BC,AB = AD = BC = 2√2,
∵E,F分别是边AB,BC的中点,
∴AE = CF = $\frac{1}{2}$×2√2 = √2,
∵点H是FD的中点,
∴DH = FH,
∵AD//BC,
∴∠DPH = ∠FCH,又
∵∠DHP = ∠FHC,
∴△PDH≌△CFH(AAS),
∴PD = CF = √2,PH = CH,即H是CD的中点,
∴AP = AD - PD = √2,
∴PE = $\sqrt{AP² + AE²}$ = $\sqrt{(√2)² + (√2)²}$ = 2,
∵点G,H分别是EC,CP的中点,
∴GH = $\frac{1}{2}$EP = 1。


【解法二】如图2,连接GF,可得GF = $\frac{1}{2}$BE = $\frac{\sqrt{2}}{2}$,GF//BE。作GM⊥DC于M,可得四边形GFCM为矩形,所以CM = $\frac{\sqrt{2}}{2}$,GM = √2,延长GH交CD于N,可得△GHF≌△NHD,所以DN = GF = $\frac{\sqrt{2}}{2}$,GH = HN = $\frac{1}{2}$GN,所以MN = CD - DN - CM = √2,由勾股定理可求出GN = 2,从而得到GH = 1。
【解法三】如图3,连接EH并延长,交CD于点M,连接FG并延长,交EH于点O,交AD于点N。易知△OGH为等腰直角三角形,OH = $\frac{1}{4}$AD = $\frac{\sqrt{2}}{2}$,所以GH = 1。


【解法四】如图4,连接FG并延长至点O,使OG = GF,连接BD,易知点O为正方形对角线的交点,GH是△OFD的中位线,所以GH = $\frac{1}{2}$OD = $\frac{1}{4}$BD = 1。
【解法五】如图5,建立如图所示的平面直角坐标系。易知E(0,√2),C(2√2,0),F(√2,0),D(2√2,2√2),所以G(√2,$\frac{\sqrt{2}}{2}$),H($\frac{3\sqrt{2}}{2}$,√2),所以GH = $\sqrt{(\frac{3\sqrt{2}}{2} - \sqrt{2})² + (\sqrt{2} - \frac{\sqrt{2}}{2})²}$ = 1。


【解法六】如图6,根据图形特性,将图形放在格点图中,小正方形的边长为$\frac{\sqrt{2}}{2}$,观察可得GH = 1。
答案 1
解析 【解法一】连接CH并延长交AD于P,连接PE,如图1,
∵四边形ABCD是正方形,且边长为2√2,
∴∠A = 90°,AD//BC,AB = AD = BC = 2√2,
∵E,F分别是边AB,BC的中点,
∴AE = CF = $\frac{1}{2}$×2√2 = √2,
∵点H是FD的中点,
∴DH = FH,
∵AD//BC,
∴∠DPH = ∠FCH,又
∵∠DHP = ∠FHC,
∴△PDH≌△CFH(AAS),
∴PD = CF = √2,PH = CH,即H是CD的中点,
∴AP = AD - PD = √2,
∴PE = $\sqrt{AP² + AE²}$ = $\sqrt{(√2)² + (√2)²}$ = 2,
∵点G,H分别是EC,CP的中点,
∴GH = $\frac{1}{2}$EP = 1。


【解法二】如图2,连接GF,可得GF = $\frac{1}{2}$BE = $\frac{\sqrt{2}}{2}$,GF//BE。作GM⊥DC于M,可得四边形GFCM为矩形,所以CM = $\frac{\sqrt{2}}{2}$,GM = √2,延长GH交CD于N,可得△GHF≌△NHD,所以DN = GF = $\frac{\sqrt{2}}{2}$,GH = HN = $\frac{1}{2}$GN,所以MN = CD - DN - CM = √2,由勾股定理可求出GN = 2,从而得到GH = 1。
【解法三】如图3,连接EH并延长,交CD于点M,连接FG并延长,交EH于点O,交AD于点N。易知△OGH为等腰直角三角形,OH = $\frac{1}{4}$AD = $\frac{\sqrt{2}}{2}$,所以GH = 1。


【解法四】如图4,连接FG并延长至点O,使OG = GF,连接BD,易知点O为正方形对角线的交点,GH是△OFD的中位线,所以GH = $\frac{1}{2}$OD = $\frac{1}{4}$BD = 1。
【解法五】如图5,建立如图所示的平面直角坐标系。易知E(0,√2),C(2√2,0),F(√2,0),D(2√2,2√2),所以G(√2,$\frac{\sqrt{2}}{2}$),H($\frac{3\sqrt{2}}{2}$,√2),所以GH = $\sqrt{(\frac{3\sqrt{2}}{2} - \sqrt{2})² + (\sqrt{2} - \frac{\sqrt{2}}{2})²}$ = 1。


【解法六】如图6,根据图形特性,将图形放在格点图中,小正方形的边长为$\frac{\sqrt{2}}{2}$,观察可得GH = 1。
11.(12分)如图,在$□ ABCD$中,对角线AC与BD相交于点O,$△ABO$是等边三角形,$AB= 1$.
(1)求证:$□ ABCD$是矩形.
(2)求矩形ABCD的面积.
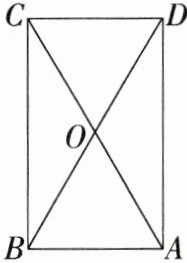
(1)求证:$□ ABCD$是矩形.
(2)求矩形ABCD的面积.

答案:
解析
(1)证明:
∵△ABO是等边三角形,
∴OA = OB = AB,
∵四边形ABCD是平行四边形,
∴OA = OC,OB = OD,
∴OA = OC = OB = OD,
∴AC = BD,
∴四边形ABCD是矩形。
(2)
∵四边形ABCD是矩形,
∴∠ABC = 90°,AC = 2AO,
∵AB = 1,
∴AO = 1,
∴AC = 2,由勾股定理得BC = $\sqrt{AC² - AB²}$ = $\sqrt{2² - 1²}$ = √3,
∴矩形ABCD的面积 = 1×√3 = √3。
(1)证明:
∵△ABO是等边三角形,
∴OA = OB = AB,
∵四边形ABCD是平行四边形,
∴OA = OC,OB = OD,
∴OA = OC = OB = OD,
∴AC = BD,
∴四边形ABCD是矩形。
(2)
∵四边形ABCD是矩形,
∴∠ABC = 90°,AC = 2AO,
∵AB = 1,
∴AO = 1,
∴AC = 2,由勾股定理得BC = $\sqrt{AC² - AB²}$ = $\sqrt{2² - 1²}$ = √3,
∴矩形ABCD的面积 = 1×√3 = √3。
12.「2023湖北十堰中考」(13分)如图,$□ ABCD$的对角线AC,BD交于点O,分别以点B,C为圆心,$\frac {1}{2}AC,\frac {1}{2}BD$的长为半径画弧,两弧交于点P,连接BP,CP.
(1)试判断四边形BPCO的形状,并说明理由.
(2)当$□ ABCD$的对角线满足什么条件时,四边形BPCO是正方形?
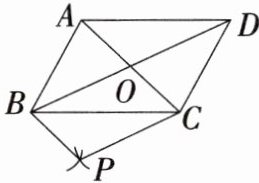
(1)试判断四边形BPCO的形状,并说明理由.
(2)当$□ ABCD$的对角线满足什么条件时,四边形BPCO是正方形?

答案:
解析
(1)四边形BPCO为平行四边形。理由:
∵四边形ABCD为平行四边形,
∴OC = OA = $\frac{1}{2}$AC,OB = OD = $\frac{1}{2}$BD,
∵分别以点B,C为圆心,$\frac{1}{2}$AC,$\frac{1}{2}$BD的长为半径画弧,两弧交于点P,
∴OB = CP,BP = OC,
∴四边形BPCO为平行四边形。
(2)当AC⊥BD,AC = BD时,四边形BPCO为正方形。
∵AC⊥BD,
∴∠BOC = 90°,
∴□BPCO为矩形。
∵AC = BD,OB = $\frac{1}{2}$BD,OC = $\frac{1}{2}$AC,
∴OB = OC,
∴矩形BPCO为正方形。
(1)四边形BPCO为平行四边形。理由:
∵四边形ABCD为平行四边形,
∴OC = OA = $\frac{1}{2}$AC,OB = OD = $\frac{1}{2}$BD,
∵分别以点B,C为圆心,$\frac{1}{2}$AC,$\frac{1}{2}$BD的长为半径画弧,两弧交于点P,
∴OB = CP,BP = OC,
∴四边形BPCO为平行四边形。
(2)当AC⊥BD,AC = BD时,四边形BPCO为正方形。
∵AC⊥BD,
∴∠BOC = 90°,
∴□BPCO为矩形。
∵AC = BD,OB = $\frac{1}{2}$BD,OC = $\frac{1}{2}$AC,
∴OB = OC,
∴矩形BPCO为正方形。
13.「2025山东济南章丘月考节选」(15分)如图,四边形ABCD为正方形,E为对角线AC上一点,连接DE,BE.过点E作$EF⊥DE$,交边BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形.
(2)若正方形ABCD的边长为9,$CG= 3\sqrt {2}$,求正方形DEFG的边长.
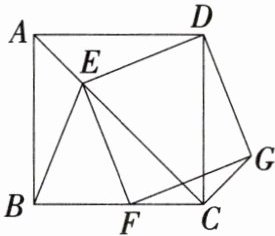
(1)求证:矩形DEFG是正方形.
(2)若正方形ABCD的边长为9,$CG= 3\sqrt {2}$,求正方形DEFG的边长.

答案:
解析
(1)证明:如图1,作EM⊥BC于M,EN⊥CD于N,易知四边形EMCN是矩形,

∴∠MEN = 90°,
∵点E是正方形ABCD对角线上的点,
∴EM = EN,
∵∠DEF = 90°,
∴∠DEN = ∠MEF = 90° - ∠FEN,在△DEN和△FEM中,{∠DNE = ∠FME = 90°,EN = EM,∠DEN = ∠FEM},
∴△DEN≌△FEM(ASA),
∴EF = DE,
∴矩形DEFG是正方形。
(2)
∵四边形DEFG和四边形ABCD是正方形,
∴DE = DG,AD = DC,
∵∠CDG + ∠CDE = ∠ADE + ∠CDE = 90°,
∴∠CDG = ∠ADE,在△ADE和△CDG中,{AD = CD,∠ADE = ∠CDG,DE = DG},
∴△ADE≌△CDG(SAS),
∴AE = CG,∠DAE = ∠DCG = 45°,
∵∠ACD = 45°,
∴∠ACG = ∠ACD + ∠DCG = 90°,
∴CE⊥CG,
∴CE + CG = CE + AE = AC = √2AB = 9√2。
∵CG = 3√2,
∴CE = 6√2;如图2,连接EG,

∴EG = $\sqrt{CE² + CG²}$ = $\sqrt{72 + 18}$ = 3√10,
∴DE = $\frac{EG}{\sqrt{2}}$ = 3√5,
∴正方形DEFG的边长为3√5。
解析
(1)证明:如图1,作EM⊥BC于M,EN⊥CD于N,易知四边形EMCN是矩形,

∴∠MEN = 90°,
∵点E是正方形ABCD对角线上的点,
∴EM = EN,
∵∠DEF = 90°,
∴∠DEN = ∠MEF = 90° - ∠FEN,在△DEN和△FEM中,{∠DNE = ∠FME = 90°,EN = EM,∠DEN = ∠FEM},
∴△DEN≌△FEM(ASA),
∴EF = DE,
∴矩形DEFG是正方形。
(2)
∵四边形DEFG和四边形ABCD是正方形,
∴DE = DG,AD = DC,
∵∠CDG + ∠CDE = ∠ADE + ∠CDE = 90°,
∴∠CDG = ∠ADE,在△ADE和△CDG中,{AD = CD,∠ADE = ∠CDG,DE = DG},
∴△ADE≌△CDG(SAS),
∴AE = CG,∠DAE = ∠DCG = 45°,
∵∠ACD = 45°,
∴∠ACG = ∠ACD + ∠DCG = 90°,
∴CE⊥CG,
∴CE + CG = CE + AE = AC = √2AB = 9√2。
∵CG = 3√2,
∴CE = 6√2;如图2,连接EG,

∴EG = $\sqrt{CE² + CG²}$ = $\sqrt{72 + 18}$ = 3√10,
∴DE = $\frac{EG}{\sqrt{2}}$ = 3√5,
∴正方形DEFG的边长为3√5。
查看更多完整答案,请扫码查看


