《2025年5年中考3年模拟九年级数学上册北师大版》

3.「2024湖北巴东期中」如图1,O为正方形ABCD对角线的交点,点E,F在正方形边BC,CD上,BE= CF,连接OE,OF,EF.
(1)求证：∠EOF= 90°.
(2)如图2,若M为CD的中点,N为BC的中点,MN与EF交于点K,请探究点K是否平分EF,说明理由.

答案：
3.解析　
(1)证明:
∵四边形ABCD为正方形，
∴OB=OC,∠BOC=90°,∠OBC=∠OCD=45°。在△OBE和△OCF中,$\begin{cases} OB=OC \\ ∠OBE=∠OCF \\ BE=CF \end{cases}$,
∴△OBE≌△OCF(SAS),
∴∠BOE=∠COF,
∴∠BOE+∠EOC=∠COF+∠EOC,
∴∠BOC=∠EOF。
∵∠BOC=90°,
∴∠EOF=90°。
(2)点K平分EF。理由:过点E作EQ⊥BC交直线MN于点Q。

∵M为CD的中点,N为BC的中点，
∴MN是△BCD的中位线，
∴MN//BD,
∴∠MNC=∠DBC=45°,∠NMC=∠BDC=45°,
∴∠ENQ=∠MNC=45°。
∵EQ⊥BC,
∴∠QEN=90°,
∴∠EQN=∠ENQ=45°,
∴EQ=EN。
∵$BN=\frac{1}{2}BC=\frac{1}{2}CD=CM$,BE=CF,
∴EN=FM,
∴EQ=FM。在△KEQ和△KFM中,$\begin{cases} ∠EQK=∠FMK \\ ∠EKQ=∠FKM \\ EQ=FM \end{cases}$,
∴△KEQ≌△KFM(AAS),
∴KE=KF,即点K平分EF。

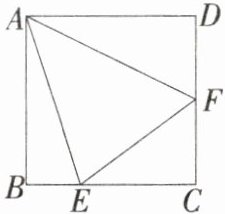
4.「2025陕西启迪中学月考」如图,在正方形ABCD中,若∠EAF= 45°,点E在BC上,点F在CD上,则下列结论：①EF= BE+DF；$②C_{△CEF}= 2AB；$③∠AEF= ∠AEB；④∠AFD= ∠AFE.其中一定成立的是( )


A.①②③④
B.①②③
C.①②④
D.②③④

答案：
4.A　由正方形“半角模型”的结论知①②③④正确。详解:延长CB至点G,使得BG=DF,连接AG,过点A作AH⊥EF于点H。

∵四边形ABCD是正方形,
∴AD=AB=BC=CD,∠D=∠ABE=∠ABG=∠BAD=90°,
∴△ADF≌△ABG(SAS),
∴AG=AF,∠2=∠3。
∵∠EAF=45°,
∴∠1+∠2=∠BAD−∠EAF=45°,
∴∠1+∠3=45°,即∠GAE=45°,
∴∠GAE=∠FAE。
∵AE=AE,
∴△GAE≌△FAE(SAS),
∴EF=GE。
∵GE=BG+BE,BG=DF,
∴EF=BE+DF,
∴①正确。
设正方形的边长为x,即AB=BC=CD=x,
∴$C_{△CEF}=CE+EF+FC=x - BE+x - DF+BE+DF=2x$,
∴$C_{△CEF}=2AB$,
∴②正确。
∵△GAE≌△FAE,
∴∠AEF=∠AEB,
∴③正确。
∵AH⊥EF,
∴∠AHE=∠ABE=90°,
∵AE=AE,∠AEB=∠AEH,
∴△AEB≌△AEH(AAS),
∴AB=AH。
∵AD=AB,
∴AH=AD,
∵AF=AF,
∴Rt△AHF≌Rt△ADF(HL),
∴∠AFD=∠AFE,
∴④正确。
综上,正确的有①②③④,故选A。

5.如图1,四边形ABCD是正方形,E是边BC的中点,∠AEF= 90°,且EF交正方形外角的平分线CF于点F,过点F作FG⊥BC于点G,连接AC.易证：AC= $\sqrt{2}$(EC+FG).(提示：取AB的中点N,连接EN)
(1)当点E是BC边上任意一点时,如图2；当点E在BC延长线上时,如图3.请直接写出AC,EC,FG的数量关系,并对图2进行证明.
(2)已知正方形ABCD的面积是27,连接AF,当△ABE中有一个内角为30°时,AF的长为______.

答案：
5.解析　
(1)题图2中,结论:$AC=\sqrt{2}(FG+EC)$。题图3中,结论:$AC=\sqrt{2}(FG - EC)$。对题图2中结论的证明过程如下:在AB上截取BM=BE,连接EM,如图。

∵四边形ABCD是正方形，
∴∠B=∠BCD=90°,AB=BC,
∴∠DCG=90°,∠EAM+∠AEB=90°。
∵BM=BE,
∴AB - BM=BC - BE,∠BME=∠BEM=45°,
∴AM=EC,∠AME=135°。
∵CF平分∠DCG,
∴∠FCG=45°,
∴∠ECF=135°,
∴∠AME=∠ECF。
∵∠AEF=90°,
∴∠FEC+∠AEB=90°,
∴∠EAM=∠FEC。在△AEM和△EFC中,$\begin{cases} ∠AME=∠ECF \\ AM=EC \\ ∠EAM=∠FEC \end{cases}$,
∴△AEM≌△EFC(ASA),
∴EM=CF。
∵$EM=\sqrt{2}BE$,$CF=\sqrt{2}FG$,
∴BE=FG。
∵$AC=\sqrt{2}BC=\sqrt{2}(BE+EC)$,
∴$AC=\sqrt{2}(FG+EC)$。
(2)当∠BAE=30°时,
∵正方形的面积为27,
∴AB=$3\sqrt{3}$,∠B=90°。在Rt△ABE中,AE=2BE,$AE^2=AB^2+BE^2$,
∴BE=3,
∴AE=2BE=6。在AB上截取BM=BE,连接EM(图略),由
(1)知△AEM≌△EFC,
∴AE=EF=6,
∴$AF=6\sqrt{2}$。
当∠AEB=30°时,同理可得$AE=EF=2AB=6\sqrt{3}$,
∴$AF=\sqrt{2}AE=6\sqrt{6}$。综上所述，AF的长为$6\sqrt{2}$或$6\sqrt{6}$。