《2025年5年中考3年模拟九年级数学上册北师大版》

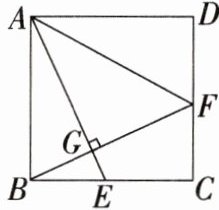
1.如图,正方形ABCD中,E是BC上的一点,连接AE,过B点作BG⊥AE,垂足为点G,延长BG交CD于点F,连接AF.
(1)求证：BE= CF.
(2)若正方形的边长是5,BE= 2,求AF的长.

答案： 1.解析　
(1)证明:
∵四边形ABCD是正方形，
∴AB=BC,∠ABE=∠BCF=90°,
∴∠BAE+∠AEB=90°。
∵BG⊥AE,
∴∠BGE=90°,
∴∠AEB+∠EBG=90°,
∴∠BAE=∠EBG,
∴△ABE≌△BCF(ASA),
∴BE=CF。
(2)
∵正方形的边长是5,
∴AB=BC=CD=5,由
(1)得BE=CF,
∵BE=2,
∴CF=2,
∴DF=CD−CF=3。
在Rt△ADF中,AF=$\sqrt{AD^2+DF^2}=\sqrt{3^2+5^2}=\sqrt{34}$。

2.如图,正方形ABCD的对角线AC,BD相交于点O,正方形A'B'C'D'的顶点A'与点O重合,边A'B'交BC于点E,边A'D'交CD于点F.
(1)求证：OE= OF.
(2)若正方形ABCD的边长为1,则两个正方形重叠部分的面积为______.
(3)在(2)的条件下,若正方形A'B'C'D'绕着点O旋转,则EF的长度何时最小？最小值是多少？请说明理由.

答案：
2.解析　
(1)证明:
∵四边形ABCD为正方形，
∴∠BOC=90°,∠OBC=∠OCD=45°,OB=OC。
∵四边形A'B'C'D'为正方形,
∴∠EOF=90°，
∵∠BOE=∠BOC−∠EOC=90°−∠EOC,∠COF=∠EOF−∠EOC=90°−∠EOC,
∴∠BOE=∠COF。
在△OBE和△OCF中,$\begin{cases} ∠BOE=∠COF \\ OB=OC \\ ∠OBC=∠OCF \end{cases}$,
∴△OBE≌△OCF(ASA),
∴OE=OF。
(2)根据过正方形对角线交点的直角模型的结论知$S_{四边形OECF}=\frac{1}{4}S_{正方形ABCD}=\frac{1}{4}$。详解如下:
∵△BOE≌△COF,
∴$S_{△BOE}=S_{△COF}$,
∴$S_{△EOC}+S_{△COF}=S_{△EOC}+S_{△BOE}$,即$S_{四边形OECF}=S_{△BOC}$。
∵正方形ABCD的边长为1,
∴正方形ABCD的面积为1,
∴$S_{△BOC}=\frac{1}{4}$,
∴两个正方形重叠部分的面积为$\frac{1}{4}$,故答案为$\frac{1}{4}$。
(3)当OE⊥BC时,EF的长度最小,最小为$\frac{\sqrt{2}}{2}$。
理由如下:连接EF,

∵∠EOF=90°,
∴$EF^2=OE^2+OF^2$,
∵OE=OF,
∴EF=$\sqrt{2}OE$,
∴要使EF最小,则OE最小。
∵当OE⊥BC时，OE的长度最小,
∴此时EF的长度最小。
当OE⊥BC时,$OE=\frac{1}{2}BC=\frac{1}{2}$,
∴$EF=\sqrt{2}OE=\frac{\sqrt{2}}{2}$。
综上,当OE⊥BC时,EF的长度最小,最小为$\frac{\sqrt{2}}{2}$。