《2025年5年中考3年模拟九年级数学上册北师大版》

1.「2024山西晋中寿阳月考」如图,$□ ABCD$中,$BE平分\angle ABC$,$CE平分\angle BCD$,$BF// CE$,$CF// BE$.
(1)求证：四边形$BECF$是矩形.
(2)若$\angle ABC= 60^{\circ}$,$BC= 6$,求四边形$BECF$的周长.

答案：
(1)证明:
∵BF//CE,CF//BE,
∴四边形BECF是平行四边形，
∵BE平分∠ABC,CE平分∠BCD,
∴∠EBC=$\frac{1}{2}$∠ABC,∠ECB=$\frac{1}{2}$∠BCD,
∵四边形ABCD是平行四边形,
∴AB//CD,
∴∠ABC+∠BCD=180°,
∴∠EBC+∠ECB=$\frac{1}{2}$(∠ABC+∠BCD)=90°,
∴∠BEC=90°,
∴平行四边形BECF是矩形.
(2)
∵BE平分∠ABC,∠ABC=60°,
∴∠EBC=30°,由
(1)可知,∠BEC=90°,
∴CE=$\frac{1}{2}$BC=3,
∴BE=$\sqrt{BC^2 - CE^2} = \sqrt{6^2 - 3^2} = 3\sqrt{3}$,
∵四边形BECF是矩形，
∴CF=BE=3√3,BF=CE=3,
∴四边形BECF的周长=2(BE+CE)=2BE+2CE=$6\sqrt{3}+6$.

2.「★☆」如图,矩形$ABCD$中,$AB= 6$,$AD= 8$,且有一点$P从B点沿BD往D$点移动,若过$P点作AB的垂线交AB于E$点,过$P点作AD的垂线交AD于F$点,则$EF$长的最小值为( )


A.$\frac{14}{5}$
B.$\frac{24}{5}$
C.5
D.7

答案：
B　如图,连接AP、EF,
　　　　　　　
∵PE⊥AB,PF⊥AD,
∴∠AEP=∠AFP=90°,
∵四边形ABCD是矩形，
∴∠BAD=90°.
∴四边形AEPF为矩形.
∴AP=EF;
∴要求EF长的最小值就是求AP长的最小值.
∵点P从B点沿BD往D点移动，
∴当AP⊥BD时,AP长取最小值.
在Rt△BAD中,
∵∠BAD=90°,AB=6,AD=8,
∴BD=$\sqrt{AB^2 + AD^2} = \sqrt{6^2 + 8^2} = \sqrt{100} = 10$.
当AP⊥BD时,
∵$S_{\triangle ABD} = \frac{1}{2}AB·AD = \frac{1}{2}AP·BD$,
∴AP=$\frac{AB·AD}{BD} = \frac{6×8}{10} = \frac{24}{5}$,
∴EF长的最小值为$\frac{24}{5}$.

3.「2024甘肃兰州中考,★☆」如图,在$\triangle ABC$中,$AB= AC$,$D是BC$的中点,$CE// AD$,$AE\perp AD$,$EF\perp AC$.
(1)求证：四边形$ADCE$是矩形.
(2)若$BC= 4$,$CE= 3$,求$EF$的长.

答案：
(1)证明:
∵在△ABC中,AB=AC,D是BC的中点，
∴AD⊥BC,即∠ADC=∠ADB=90°,
∵CE//AD,
∴∠ECD=∠ADB=90°,
∵AE⊥AD,
∴∠EAD=90°,
∴∠ADC=∠ECD=∠EAD=90°,
∴四边形ADCE是矩形.
(2)
∵在△ABC中,AB=AC,D是BC的中点,BC=4,
∴BD=CD=$\frac{1}{2}$BC=2.由
(1)可知四边形ADCE是矩形,
∴AE=CD=2,∠AEC=90°.在Rt△AEC中,AE=2,CE=3,由勾股定理得AC=$\sqrt{AE^2 + CE^2} = \sqrt{13}$
∵EF⊥AC,
∴$S_{\triangle AEC} = \frac{1}{2}AC·EF = \frac{1}{2}AE·CE$,
∴EF=$\frac{AE·CE}{AC} = \frac{2×3}{\sqrt{13}} = \frac{6\sqrt{13}}{13}$.

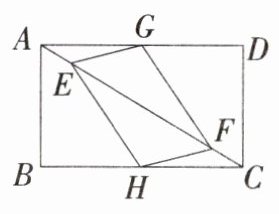
4.「2025浙江金华横店八校联考,★☆」在矩形$ABCD$中,$AB= 6$,$BC= 8$,$E$、$F是对角线AC$上的两个动点,分别从$A$、$C$同时出发相向而行,速度均为每秒1个单位长度,运动时间为$t$秒,其中$0\leqslant t\leqslant 10$.
(1)若$G$,$H分别是AD$,$BC$的中点,则四边形$EGFH$一定是怎样的四边形($E$、$F$相遇时除外)？
答：______.(直接填空,不用说理)
(2)在(1)的条件下,若四边形$EGFH$为矩形,求$t$的值.
(3)在(1)的条件下,若$G向D$点运动,$H向B$点运动,且与点$E$,$F$以相同的速度同时出发,则求四边形$EGFH为菱形时t$的值.

答案：

(1)平行四边形.
详解:由题意得AE=CF=t,
∵四边形ABCD是矩形，
∴AD//BC,AD=BC,
∴∠GAE=∠HCF,
∵G,H分别是AD,BC的中点，
∴AG=$\frac{1}{2}$AD,CH=$\frac{1}{2}$BC,
∴AG=CH,
∴△AEG≌△CFH(SAS),
∴EG=FH,∠AEG=∠CFH,
∴∠FEG=∠EFH,
∴EG//HF,
∴四边形EGFH是平行四边形,
(2)如图1,连接GH,
　　　　　　　　
由
(1)得AG=BH,AG//BH,∠B=90°,
∴四边形ABHG 是矩形,
∴GH=AB=6.当四边形EGFH是矩形时,EF=GH=6,
∵AE=CF=t,
∴EF=10−2t=6或EF=t+t−10=2t−10=6,
∴t=2或t=8.
综上,四边形EGFH为矩形时,t=2或t=8.
(3)如图2,M和N分别是AD和BC的中点，连接AH,CG,GH,AC与GH交于O,
　　　　　　　　
∵四边形EGFH为菱形，
∴GH⊥EF,OG=OH,OE=OF,
∴OA=OC,AG=AH,
∴四边形AGCH为菱形，
∴AG=CG.设AG=CG=x,则DG=8−x,由勾股定理可得$CD^2 + DG^2 = CG^2$,即$6^2 + (8 - x)^2 = x^2$,解得x=$\frac{25}{4}$,
∴MG=$\frac{25}{4}$−4=$\frac{9}{4}$,即t=$\frac{9}{4}$.
∴当t=$\frac{9}{4}$时，四边形EGFH为菱形.