《2025年优佳学案暑假活动七年级合订本》

11. 已知$\begin{cases}x + 2y = 4k,\\2x + y = 2k + 1,\end{cases}$且$x + y ＞ 0$，则$k$的取值范围是（ ）
A. $k ＞ -\dfrac{5}{4}$
B. $k ＜ -\dfrac{5}{4}$
C. $k ＜ \dfrac{1}{6}$
D. $k ＞ -\dfrac{1}{6}$

答案： D

12. 某宾馆有二人间、三人间、四人间三种客房供游客租住，某旅行团$20$人准备租用$7$间客房，若三种客房都要租用，且每间客房都住满，则租房方案有（ ）
A. 1种
B. 2种
C. 3种
D. 4种

答案： B

13. 如图，在长方形$ABCD$中放置$9$个形状、大小都相同的小长方形（尺寸如图所示，单位：$cm$），则图中阴影部分的面积为（ ）

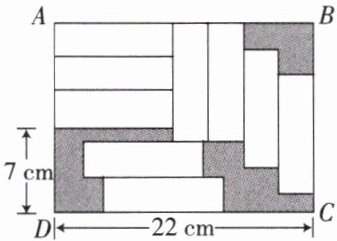
A. $82cm^{2}$
B. $64cm^{2}$
C. $60cm^{2}$
D. $54cm^{2}$

答案： A

14. 已知有理数$x$，$y$，$z$满足方程组$\begin{cases}2x - y + 3z = 3,\\2y - 4x - 4z = 0,\end{cases}$则$2x - y$等于（ ）
A. -6
B. 6
C. -3
D. 0.6

答案： A

15. $○$，$□$，$\triangle$各代表一个数，根据$○ + \triangle = 50$，$□ + \triangle = 63$，$○ + □ = 77$，求得$○ =$______。

答案： $32$

16. 定义一种运算$※$如下：$x※y = ax + by$，$a$和$b$均为常数。已知：$3※5 = 12$，$4※7 = 20$，则$2※3 =$________。

答案： 【解析】：
已知$x※y = ax + by$，且$3※5 = 12$，$4※7 = 20$，可得到方程组$\begin{cases}3a + 5b = 12&(1)\\4a + 7b = 20&(2)\end{cases}$。
为了消去$a$，给$(1)$式两边同时乘以$4$，给$(2)$式两边同时乘以$3$，得到：
$\begin{cases}12a + 20b = 48&(3)\\12a + 21b = 60&(4)\end{cases}$
用$(4)$式减去$(3)$式可得：
$(12a + 21b)-(12a + 20b)=60 - 48$
$12a + 21b - 12a - 20b = 12$
$b = 12$
把$b = 12$代入$(1)$式$3a + 5×12 = 12$，即$3a + 60 = 12$，移项可得$3a = 12 - 60=-48$，解得$a = - 16$。
所以$x※y=-16x + 12y$，则$2※3=-16×2 + 12×3=-32 + 36 = 4$。
【答案】：$4$

17. 解下列二元一次方程组：
（1）$\begin{cases}y = 2x - 1,\\2x + y - 11 = 0;\end{cases}$
（2）$\begin{cases}\dfrac{x}{2} + \dfrac{y + 1}{3} = 3,\\3x - 2(y + 1) = 6;\end{cases}$

答案： 【解析】：
（1）
将$y = 2x - 1$代入$2x + y - 11 = 0$，可得：
$2x+(2x - 1)-11 = 0$
去括号得：$2x+2x - 1 - 11 = 0$
合并同类项得：$4x-12 = 0$
移项得：$4x = 12$
系数化为$1$得：$x = 3$
把$x = 3$代入$y = 2x - 1$，得$y=2×3 - 1=6 - 1 = 5$。
所以方程组$\begin{cases}y = 2x - 1\\2x + y - 11 = 0\end{cases}$的解为$\begin{cases}x = 3\\y = 5\end{cases}$。
（2）
首先对原方程组进行化简：
方程$\frac{x}{2}+\frac{y + 1}{3}=3$两边同时乘以$6$去分母得：
$3x + 2(y + 1)=18$
原方程组$\begin{cases}\frac{x}{2}+\frac{y + 1}{3}=3\\3x - 2(y + 1)=6\end{cases}$可化为$\begin{cases}3x + 2(y + 1)=18&①\\3x - 2(y + 1)=6&②\end{cases}$
$①+②$得：
$(3x + 2(y + 1))+(3x - 2(y + 1))=18 + 6$
去括号得：$3x+2y + 2+3x - 2y - 2 = 24$
合并同类项得：$6x = 24$
系数化为$1$得：$x = 4$
把$x = 4$代入$3x - 2(y + 1)=6$得：
$3×4-2(y + 1)=6$
$12-2(y + 1)=6$
去括号得：$12-2y - 2 = 6$
$10-2y = 6$
移项得：$-2y = 6 - 10$
$-2y=-4$
系数化为$1$得：$y = 2$
所以方程组$\begin{cases}\frac{x}{2}+\frac{y + 1}{3}=3\\3x - 2(y + 1)=6\end{cases}$的解为$\begin{cases}x = 4\\y = 2\end{cases}$。
【答案】：（1）$\begin{cases}x = 3\\y = 5\end{cases}$；（2）$\begin{cases}x = 4\\y = 2\end{cases}$

18. 已知方程组$\begin{cases}ax + 5y + c = 10,①\\4x - by + 2d = 12,②\end{cases}$小明把方程①抄错了，得方程组的解为$\begin{cases}x = 1,\\y = 1;\end{cases}$小亮把方程②抄错了，得方程组的解为$\begin{cases}x = -1,\\y = -1.\end{cases}$已知方程组正确的解为$\begin{cases}x = 2,\\y = 2,\end{cases}$求$a$，$b$，$c$，$d$的值。

答案： 【解析】：
因为小明把方程①抄错了，所以小明得到的解$\begin{cases}x = 1\\y = 1\end{cases}$对于方程②是正确的，将$\begin{cases}x = 1\\y = 1\end{cases}$代入方程②$4x - by + 2d = 12$可得：
$4×1 - b×1+2d = 12$，即$4 - b + 2d = 12$，整理得$-b + 2d = 8$ ③；
小亮把方程②抄错了，所以小亮得到的解$\begin{cases}x=-1\\y = -1\end{cases}$对于方程①是正确的，将$\begin{cases}x=-1\\y = -1\end{cases}$代入方程①$ax + 5y + c = 10$可得：
$a×(-1)+5×(-1)+c = 10$，即$-a - 5 + c = 10$，整理得$-a + c = 15$ ④；
又因为方程组正确的解为$\begin{cases}x = 2\\y = 2\end{cases}$，将其代入方程①$ax + 5y + c = 10$可得：
$2a+5×2 + c = 10$，即$2a + 10 + c = 10$，整理得$2a + c = 0$ ⑤；
将$\begin{cases}x = 2\\y = 2\end{cases}$代入方程②$4x - by + 2d = 12$可得：
$4×2 - b×2+2d = 12$，即$8 - 2b + 2d = 12$，整理得$-2b + 2d = 4$ ⑥；
由③$-b + 2d = 8$与⑥$-2b + 2d = 4$组成方程组$\begin{cases}-b + 2d = 8\\-2b + 2d = 4\end{cases}$，
用$-b + 2d = 8$减去$-2b + 2d = 4$可得：
$(-b + 2d)-(-2b + 2d)=8 - 4$，
$-b + 2d + 2b - 2d = 4$，
$b = 4$；
把$b = 4$代入③$-b + 2d = 8$，得$-4 + 2d = 8$，解得$d = 6$；
由④$-a + c = 15$与⑤$2a + c = 0$组成方程组$\begin{cases}-a + c = 15\\2a + c = 0\end{cases}$，
用$2a + c = 0$减去$-a + c = 15$可得：
$(2a + c)-(-a + c)=0 - 15$，
$2a + c + a - c = -15$，
$3a = -15$，
解得$a = - 5$；
把$a = - 5$代入④$-a + c = 15$，得$-(-5)+c = 15$，解得$c = 10$。
【答案】：$a=-5$，$b = 4$，$c = 10$，$d = 6$