《2025年优佳学案暑假活动七年级合订本》

1. 下列调查中，适宜采用抽样调查的是（）
A. 企业招聘，对应聘人员进行面试
B. 调查某批次汽车的抗撞击能力
C. 了解某班学生的身高情况
D. 选拔该校短跑成绩最优的学生参加全市比赛

答案： B

2. 为调查某市 45000 名中考学生的身高情况，现随机抽取 1500 名学生进行身高数据统计分析.下列结论中正确的是（）
A. 45000 名学生是总体
B. 1500 名学生的身高是总体的一个样本
C. 每名学生是总体的一个个体
D. 以上调查是全面调查

答案： B

3. 空气的主要成分是：氮气约占 78%；氧气约占 21%；其他微量气体约占 1%. 为了直观地介绍空气中各成分的百分比，宜采用的统计图是（）
A. 扇形图
B. 条形图
C. 折线图
D. 频数分布直方图

答案： A

4. 已知 $ AB // y $ 轴，点 $ B $ 的坐标为 $ (1,3) $，若点 $ A $ 的坐标可表示为 $ (m,m + 1) $，则点 $ A $ 的坐标为（）
A. $ (1,2) $
B. $ (1,-3) $
C. $ (2,3) $
D. $ (-2,-3) $

答案： A

5. 不等式组 $ \begin{cases} 2x ＜ -4, \\ x - 2 \geq 0 \end{cases} $ 的解集在数轴上表示正确的是（）

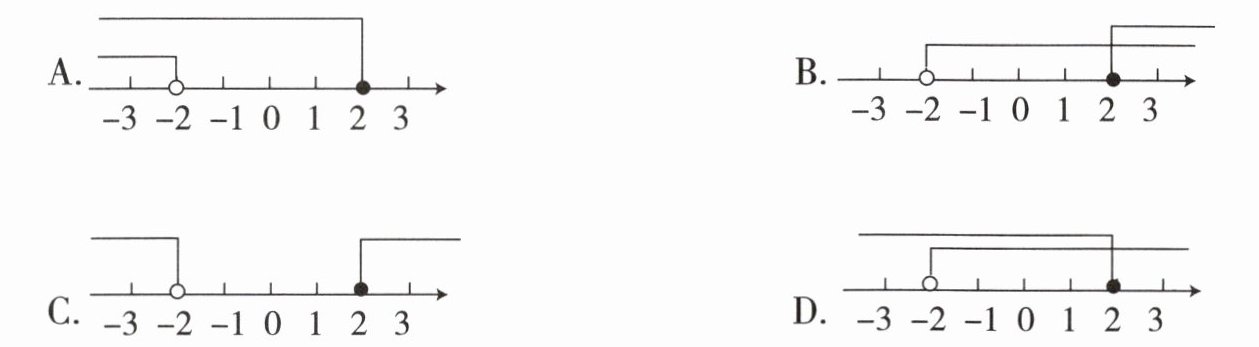
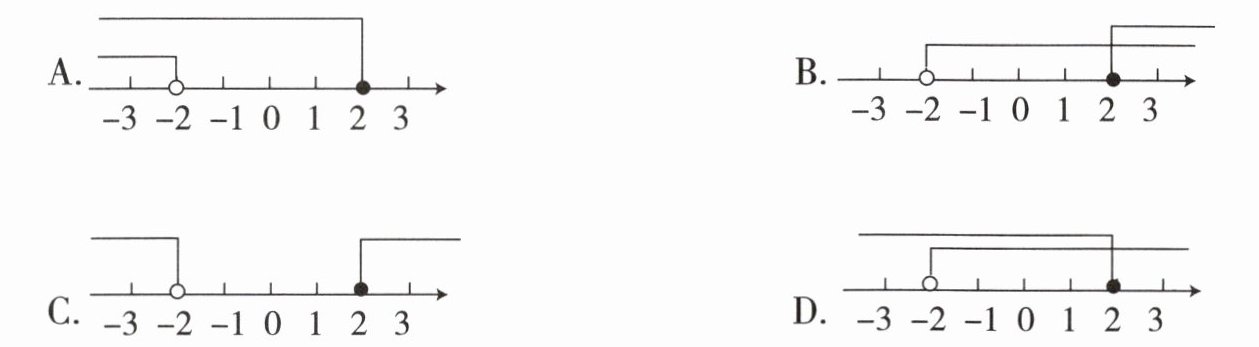
答案： D

6. 如图，点 $ E $ 在 $ AD $ 的延长线上，下列条件中能推出 $ BC // AD $的是（）

A. $ \angle 1 = \angle 2 $
B. $ \angle A = \angle 5 $
C. $ \angle A + \angle ADC = 180^\circ $
D. $ \angle 3 = \angle 4 $

答案： A

7. 若 $ x $ 是 4 的算术平方根，$ y $ 是 -8 的立方根，则 $ xy $ 的值为________.

答案： $-4$

8. 若点 $ P(3m - 1,2m) $ 在第二象限内，则 $ m $ 的取值范围是________.

答案： $0\lt m\lt \frac{1}{3}$

9. （1）计算：$ -1^4 + \sqrt[3]{64} - (-\sqrt{2}) + \sqrt{9} - |-\sqrt{2}| $.
（2）解方程：$ 9x^2 - 25 = 0 $.
（3）解方程：$ (2 - 5x)^3 = -27 $.
（4）解方程组 $ \begin{cases} x - y = 3, & ① \\ 2x - 3y = 8. & ② \end{cases} $
（5）解不等式组 $ \begin{cases} x + 1 \geq 0, \\ \dfrac{x + 1}{2} - 1 ＜ \dfrac{x}{3}, \end{cases} $ 并写出它的正整数解.

答案： 【解析】：
（1）
首先，根据幂运算规则，$-1^4$表示$1$的四次方的相反数，所以$-1^4=-1$。
然后，$\sqrt[3]{64}$，因为$4^3 = 64$，所以$\sqrt[3]{64}=4$。
$-(-\sqrt{2})=\sqrt{2}$，$\sqrt{9}=3$，$\vert-\sqrt{2}\vert=\sqrt{2}$。
则原式$=-1 + 4+\sqrt{2}+3-\sqrt{2}$，合并同类项可得$(-1 + 4+3)+(\sqrt{2}-\sqrt{2})=6$。
（2）
对于方程$9x^2 - 25 = 0$，先移项得到$9x^2 = 25$。
两边同时除以$9$，得$x^2=\frac{25}{9}$。
根据平方根的定义，$x=\pm\sqrt{\frac{25}{9}}=\pm\frac{5}{3}$。
（3）
对于方程$(2 - 5x)^3 = -27$，因为$(-3)^3=-27$，所以$2 - 5x=-3$。
移项可得$-5x=-3 - 2$，即$-5x=-5$。
两边同时除以$-5$，解得$x = 1$。
（4）
由方程①$x - y = 3$可得$x=y + 3$。
将$x=y + 3$代入方程②$2x - 3y = 8$中，得到$2(y + 3)-3y = 8$。
去括号得$2y+6 - 3y = 8$。
合并同类项得$-y+6 = 8$。
移项得$-y=8 - 6$，即$-y = 2$，解得$y=-2$。
把$y = -2$代入$x=y + 3$，得$x=-2 + 3=1$。
所以方程组的解为$\begin{cases}x = 1\\y=-2\end{cases}$。
（5）
解不等式$x + 1\geq0$，移项可得$x\geq - 1$。
解不等式$\frac{x + 1}{2}-1\lt\frac{x}{3}$，
先去分母，两边同时乘以$6$得$3(x + 1)-6\lt2x$。
去括号得$3x+3 - 6\lt2x$。
移项得$3x-2x\lt6 - 3$。
合并同类项得$x\lt3$。
所以不等式组的解集为$-1\leq x\lt3$，其正整数解为$1$，$2$。
【答案】：（1）$6$；（2）$x=\pm\frac{5}{3}$；（3）$x = 1$；（4）$\begin{cases}x = 1\\y=-2\end{cases}$；（5）不等式组的解集为$-1\leq x\lt3$，正整数解为$1$，$2$。