《2025年通城学典暑期升级训练八年级物理人教版》

4. 跨学科实践 工程实践 (常州中考)为实施流花11-1油田二次开发,中国工程师需要将导管架从陆地工厂运至海洋指定位置。
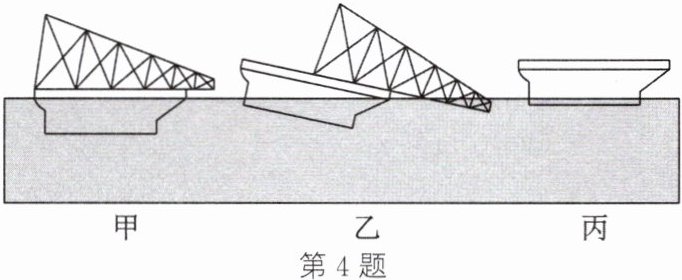
① 工程师将导管架装载在驳船上,静止时驳船排开海水的体积为$8×10^4m^3,$如图甲所示。
② 驳船将导管架运至海洋指定位置后,导管架被推入海中,如图乙所示。
③ 驳船和导管架完全分离后,静止时空驳船排开海水的体积为$5×10^4m^3,$如图丙所示。
已知导管架的体积为$3.3×10^4m^3,ρ$海水取$1.1×10^3kg/m^3,g$取10N/kg。求:
(1) 导管架受到的重力大小。
(2) 导管架和驳船完全分离后,导管架最终静止时受到的浮力大小。

答案： （1）当导管架在驳船上时，整体漂浮，所受浮力等于驳船和导管架的总重力，根据阿基米德原理算出浮力$F_{\text{浮}1}=\rho_{\text{海水}}gV_{\text{排}1}=1.1×10^{3}\ \text{kg/m}^3×10\ \text{N/kg}×8×10^{4}\ \text{m}^3=8.8×10^{8}\ \text{N}$；当导管架不在驳船上时，空驳船所受浮力等于驳船重力，根据阿基米德原理算出浮力$F_{\text{浮}2}=\rho_{\text{海水}}gV_{\text{排}2}=1.1×10^{3}\ \text{kg/m}^3×10\ \text{N/kg}×5×10^{4}\ \text{m}^3=5.5×10^{8}\ \text{N}$；故导管架的重力等于两次重力差，即等于两次浮力差，$G=F_{\text{浮}1}-F_{\text{浮}2}=8.8×10^{8}\ \text{N}-5.5×10^{8}\ \text{N}=3.3×10^{8}\ \text{N}$ （2）导管架质量$m=\frac{G}{g}=\frac{3.3×10^{8}\ \text{N}}{10\ \text{N/kg}}=3.3×10^{7}\ \text{kg}$，其密度$\rho=\frac{m}{V}=\frac{3.3×10^{7}\ \text{kg}}{3.3×10^{4}\ \text{m}^3}=1×10^{3}\ \text{kg/m}^3$，小于海水密度$1.1×10^{3}\ \text{kg/m}^3$，故导管架会漂浮；漂浮时，所受浮力等于重力，故浮力大小为$3.3×10^{8}\ \text{N}$

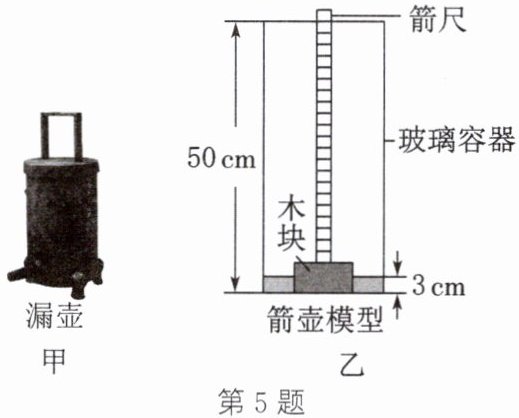
5. (泰安中考)古代有一种计时器称为“漏刻”,其计时原理是通过漏壶或箭壶中水量的均匀变化来度量时间。图甲为我国国家博物馆收藏的西汉时
期的计时工具青铜漏壶。图乙为某同学设计的计时工具箭壶模型,该模型由薄壁圆柱形玻璃容器、长方体木块(不吸水)和标有刻度的箭尺构成,箭尺重力忽略不计,其底部与木块相连,向容器内均匀注水,可使箭尺和木块随水面匀速竖直上升,从而计时。已知容器高为50cm,底面积为$700cm^2;$木块重1.5N,高为5cm。初始状态下,容器内有部分水,刚好使木块在浮力作用下与容器底部脱离接触,此时水深为3cm;工作状态下,当木块上升至上表面刚好与容器上沿相平时,一个计时周期结束。g取10N/kg,ρ水$= 1.0×10^3kg/m^3,$不计容器底和容器壁的厚度。求:
(1) 初始状态下木块受到的浮力。
(2) 木块的密度。
(3) 计时周期结束时木块底部受到的水的压强和容器内水的质量。

答案： （1）初始状态下，木块漂浮，受到的浮力$F_{\text{浮}}=G_{\text{木}}=1.5\ \text{N}$ （2）初始状态下，由题知，$V_{\text{排}}=\frac{3}{5}V_{\text{木}}$ ①，由$F_{\text{浮}}=G_{\text{木}}$，可得$\rho_{\text{水}}gV_{\text{排}}=\rho_{\text{木}}gV_{\text{木}}$ ②，由①②可得木块的密度$\rho_{\text{木}}=\frac{3}{5}\rho_{\text{水}}=\frac{3}{5}×1.0×10^{3}\ \text{kg/m}^3=0.6×10^{3}\ \text{kg/m}^3$ （3）由题知，刚好使木块在浮力作用下与容器底部脱离接触时，水深为$3\ \text{cm}$，即木块漂浮时其浸入水中的深度$h_{\text{浸}}=3\ \text{cm}$，则此时木块露出水面的高度$h_{\text{露}}=h_{\text{木块}}-h_{\text{浸}}=5\ \text{cm}-3\ \text{cm}=2\ \text{cm}$，根据题意，计时周期结束时，容器内水深$h_{\text{水}}=H-h_{\text{露}}=50\ \text{cm}-2\ \text{cm}=48\ \text{cm}$，木块底部所处的深度$h_{1}=h_{\text{浸}}=3\ \text{cm}=0.03\ \text{m}$，木块底部受到的水的压强$p_{\text{水}}=\rho_{\text{水}}gh_{1}=1.0×10^{3}\ \text{kg/m}^3×10\ \text{N/kg}×0.03\ \text{m}=300\ \text{Pa}$，水的体积与木块排开水的体积之和$V_{\text{总}}=Sh_{\text{水}}=700\ \text{cm}^2×48\ \text{cm}=33600\ \text{cm}^3$，由$F_{\text{浮}}=\rho_{\text{水}}gV_{\text{排}}$得，木块排开水的体积$V_{\text{排}}=\frac{F_{\text{浮}}}{\rho_{\text{水}}g}=\frac{1.5\ \text{N}}{1.0×10^{3}\ \text{kg/m}^3×10\ \text{N/kg}}=1.5×10^{-4}\ \text{m}^3=150\ \text{cm}^3$，水的体积$V_{\text{水}}=V_{\text{总}}-V_{\text{排}}=33600\ \text{cm}^3-150\ \text{cm}^3=33450\ \text{cm}^3$，由$\rho=\frac{m}{V}$可知水的质量$m_{\text{水}}=\rho_{\text{水}}V_{\text{水}}=1.0\ \text{g/cm}^3×33450\ \text{cm}^3=33450\ \text{g}=33.45\ \text{kg}$