《2025年通城学典暑期升级训练延边大学出版社八年级数学华师大版》

1. 如图,在$□ ABCD$中,若$∠A= 110^{\circ }$,则$∠B$的度数为( )

A.$110^{\circ }$
B.$70^{\circ }$
C.$55^{\circ }$
D.$35^{\circ }$

答案： 【解析】：
本题考查的知识点是平行四边形的邻角互补性质。在平行四边形中，邻角是互补的，即它们的角度和为$180^\circ$。题目给出$∠A = 110^\circ$，要求找出$∠B$的度数。由于$∠A$和$∠B$是平行四边形中的邻角，根据邻角互补的性质，有$∠A + ∠B = 180^\circ$。将$∠A = 110^\circ$代入，得到$∠B = 180^\circ - 110^\circ = 70^\circ$。
【答案】：B. $70^\circ$。

2.(益阳中考)如图,$□ ABCD$的对角线AC、BD相交于点O.若$AC= 6,BD= 8$,则AB的长可能是( )

A.10
B.8
C.7
D.6

答案： 【解析】：
本题可根据平行四边形的性质求出$OA$与$OB$的长度，再利用三角形三边关系来确定$AB$的取值范围，最后据此判断选项。
步骤一：根据平行四边形的性质求出$OA$与$OB$的长度
平行四边形的对角线互相平分，已知在平行四边形$ABCD$中，对角线$AC = 6$，$BD = 8$，且$AC$与$BD$相交于点$O$，所以$OA=\frac{1}{2}AC$，$OB=\frac{1}{2}BD$。
将$AC = 6$，$BD = 8$代入可得：$OA=\frac{1}{2}×6 = 3$，$OB=\frac{1}{2}×8 = 4$。
步骤二：利用三角形三边关系确定$AB$的取值范围
在$\triangle AOB$中，根据三角形三边关系“任意两边之和大于第三边，任意两边之差小于第三边”，可得$OB - OA\lt AB\lt OA + OB$。
将$OA = 3$，$OB = 4$代入可得：$4 - 3\lt AB\lt 4 + 3$，即$1\lt AB\lt 7$。
步骤三：结合$AB$的取值范围判断选项
逐一分析各个选项：
选项A：$10\gt7$，不满足$1\lt AB\lt 7$，所以该选项错误。
选项B：$8\gt7$，不满足$1\lt AB\lt 7$，所以该选项错误。
选项C：$7$不满足$1\lt AB\lt 7$（$AB$不能等于$7$），所以该选项错误。
选项D：$1\lt 6\lt 7$，满足$1\lt AB\lt 7$，所以该选项正确。
【答案】：D

3.(衡阳中考)如图,在四边形ABCD中,对角线AC、BD相交于点O.下列条件中,不能判定四边形ABCD为平行四边形的是( )

A.$AB// DC,AD// BC$
B.$AB= DC,AD= BC$
C.$AB// DC,AD= BC$
D.$OA= OC,OB= OD$

答案： 【解析】：本题考查平行四边形的判定定理。
A选项：$AB// DC$，$AD// BC$，根据平行四边形的定义（两组对边分别平行的四边形是平行四边形），可以判定四边形$ABCD$是平行四边形，所以A选项不符合题意。
B选项：$AB = DC$，$AD = BC$，根据平行四边形的判定定理（两组对边分别相等的四边形是平行四边形），可以判定四边形$ABCD$是平行四边形，所以B选项不符合题意。
C选项：$AB// DC$，$AD = BC$，一组对边平行，另一组对边相等的四边形不一定是平行四边形，有可能是等腰梯形等，所以不能判定四边形$ABCD$是平行四边形，C选项符合题意。
D选项：$OA = OC$，$OB = OD$，根据平行四边形的判定定理（对角线互相平分的四边形是平行四边形），可以判定四边形$ABCD$是平行四边形，所以D选项不符合题意。
【答案】：C

4.(朝阳中考)将一块三角尺按如图所示的方式放置在一张平行四边形的纸片上,$∠EFG= 90^{\circ },∠EGF= 60^{\circ },∠AEF= 50^{\circ }$,则$∠EGC$的度数为( )

A.$100^{\circ }$
B.$80^{\circ }$
C.$70^{\circ }$
D.$60^{\circ }$

答案： 解：
∵ 四边形ABCD是平行四边形，
∴ AD//BC，
∴ ∠AEF=∠EGB=50°（两直线平行，内错角相等）。
∵ ∠EFG=90°，∠EGF=60°，
∴ 在△EFG中，∠FEG=180°-∠EFG-∠EGF=30°。
∵ ∠EGB+∠FEG+∠EGC=180°（平角定义），
∴ ∠EGC=180°-∠EGB-∠FEG=180°-50°-30°=100°。
答案：A

5. 如图,在$□ ABCD$中,$AB= 6cm,AD= 8cm$,AC、BD相交于点O,$OE⊥BD$交AD于点E,则$\triangle ABE$的周长为( )

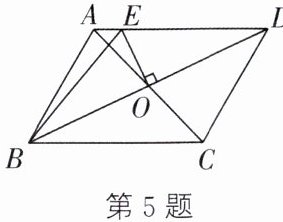
A.12 cm
B.14 cm
C.16 cm
D.28 cm
平行四边形1
时间：90分钟)

答案： 解：
∵四边形ABCD是平行四边形，
∴BO=DO。
∵OE⊥BD，
∴OE垂直平分BD，
∴BE=DE。
∵AB=6cm，AD=8cm，
∴△ABE的周长=AB+AE+BE=AB+AE+DE=AB+AD=6+8=14cm。
答案：B

6.(赤峰中考)如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合部分构成一个四边形ABCD.任意转动其中一张纸条,则下列结论中,一定成立的是( )

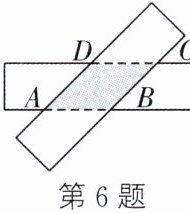
A.四边形ABCD的周长不变
B.$AD= CD$
C.四边形ABCD的面积不变
D.$AD= BC$

答案： 【解析】：本题可根据平行四边形的判定与性质，对各选项逐一进行分析。
选项A：判断四边形$ABCD$的周长是否不变
由于随意转动其中一张纸条，两张纸条的夹角会发生变化，那么$AB$与$BC$的长度会改变，四边形$ABCD$的周长$C = 2(AB + BC)$，所以周长会改变，该选项错误。
选项B：判断$AD = CD$是否一定成立
虽然四边形$ABCD$是平行四边形，但平行四边形的邻边不一定相等，即$AD$与$CD$不一定相等，该选项错误。
选项C：判断四边形$ABCD$的面积是否不变
四边形$ABCD$的面积$S = AB× h$（$h$为$AB$边上的高），转动纸条时，两张纸条的夹角改变，$AB$边上的高$h$会发生变化，$AB$的长度也可能改变，所以面积会改变，该选项错误。
选项D：判断$AD = BC$是否一定成立
因为两张纸条的对边平行，即$AB// CD$，$AD// BC$，根据平行四边形的定义：两组对边分别平行的四边形是平行四边形，可知四边形$ABCD$是平行四边形。
再根据平行四边形的性质：平行四边形的对边相等，所以$AD = BC$，该选项正确。
【答案】：D

7. 如图,在$□ ABCD$中,$AB= 5,AD= 7$,AE平分$∠BAD$交BC于点E,过点D作$DG⊥AE$于点G并延长,交BC于点F,则线段EF的长为( )

A.2
B.$\frac {5}{2}$
C.3
D.4

答案： 解：
∵四边形ABCD是平行四边形，
∴AD//BC，AD=BC=7，AB=CD=5，
∴∠DAE=∠AEB．
∵AE平分∠BAD，
∴∠BAE=∠DAE，
∴∠BAE=∠AEB，
∴BE=AB=5．
∵DG⊥AE，
∴∠AGD=∠AGF=90°．
在△AGD和△AGF中，
∠GAD=∠GAF（AE平分∠BAD），
AG=AG（公共边），
∠AGD=∠AGF=90°，
∴△AGD≌△AGF（ASA），
∴AD=AF=7．
∵AD//BC，
∴∠ADF=∠DFC．
又
∵∠AGD=∠EGF=90°，∠ADF=∠EFG（对顶角相等），
∴∠DFC=∠EFG，
∴EF=EC．
∵EC=BC-BE=7-5=2，
∴EF=2．
答案：A

8. 如图,在平面直角坐标系中,$□ OABC$的边OC落在x轴的正半轴上,点$C(4,0)$、$B(6,2)$.直线$y= 2x+1$以每秒3个单位的速度向下平移,经过一段时间,该直线将$□ OABC$的面积平分,则经过的时间为( )

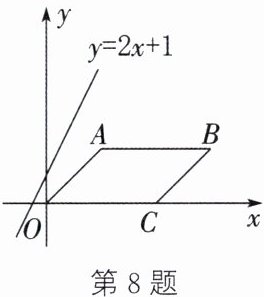
A.1秒
B.2秒
C.3秒
D.4秒

答案： 【解析】：本题可先求出平行四边形$OABC$的对角线交点坐标，再根据直线平移的性质求出平移后的直线方程，进而求出平移的时间。
求出平行四边形$OABC$对角线交点坐标：
对于平行四边形，其对角线互相平分，即对角线交点是两条对角线的中点。
已知$O(0,0)$，$B(6,2)$，根据中点坐标公式：若有两点$M(x_1,y_1)$，$N(x_2,y_2)$，则它们的中点$P$的坐标为$(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2})$，可得平行四边形$OABC$对角线$OB$与$AC$的交点坐标为$(\frac{0+6}{2},\frac{0+2}{2})=(3,1)$。
求出直线$y = 2x + 1$平移后的方程：
设直线$y = 2x + 1$向下平移$3t$个单位（因为速度是每秒$3$个单位，时间为$t$秒），根据直线平移规律“上加下减”（即直线$y=kx+b$向上平移$m$个单位得到$y=kx+b+m$，向下平移$m$个单位得到$y=kx+b-m$），则平移后的直线方程为$y = 2x + 1 - 3t$。
根据直线平分平行四边形面积求出$t$的值：
因为平移后的直线将平行四边形$OABC$的面积平分，而平行四边形的对角线交点是平行四边形的对称中心，过对称中心的直线将平行四边形面积平分，所以平移后的直线$y = 2x + 1 - 3t$经过点$(3,1)$。
将点$(3,1)$代入$y = 2x + 1 - 3t$可得：
$1=2×3 + 1 - 3t$
$1=6 + 1 - 3t$
$1=7 - 3t$
$3t=7 - 1$
$3t=6$
$t = 2$
所以经过的时间为$2$秒。
【答案】：B。

9.(鸡西中考)如图,在四边形ABCD中,$AD// BC$,在不添加任何辅助线的情况下,请你添加一个条件：____,使四边形ABCD是

答案： 解：添加条件：AD=BC。
证明：
∵AD//BC，AD=BC，
∴四边形ABCD是平行四边形（一组对边平行且相等的四边形是平行四边形）。
或添加条件：AB//CD。
证明：
∵AD//BC，AB//CD，
∴四边形ABCD是平行四边形（两组对边分别平行的四边形是平行四边形）。
或添加条件：∠A=∠C。
证明：
∵AD//BC，
∴∠A+∠B=180°，
∵∠A=∠C，
∴∠C+∠B=180°，
∴AB//CD，
∵AD//BC，AB//CD，
∴四边形ABCD是平行四边形（两组对边分别平行的四边形是平行四边形）。
或添加条件：∠B=∠D。
证明：
∵AD//BC，
∴∠A+∠B=180°，
∵∠B=∠D，
∴∠A+∠D=180°，
∴AB//CD，
∵AD//BC，AB//CD，
∴四边形ABCD是平行四边形（两组对边分别平行的四边形是平行四边形）。
（答案不唯一，以上任填一个即可）